Epipolor Geometry
3D point estimation을 수행할 때, 왜 2장의 이미지가 필요할까?
카메라 투영 시 3D에서 2D로의 mapping 관계는 이전 글에서 많이 다뤘다. 그러나 2D에서 3D로의 mapping 관계를 풀기 위해 intrinsic과 extrinsic matrix를 활용할 수 있지만, extrinsic을 알지 못하는 경우가 너무 많다. 사실 이 extrinsic matrix를 안다는 것은 실제 3d point를 안다는 것과 같다. SLAM이나 mapping 기술들 대부분이 결국 extrinsic를 구하는 자체가 목적이 된다.
그렇다면 Depth값을 이미 알고 있다면, SLAM을 굳이 사용하지 않아도 되는 거라 생각할 수 있다. 그러나 Depth카메라의 경우 노이즈가 많이 생겨서 오히려 더 부정확하게 3D point를 추정될 수 있다. 그래서 여러 장의 이미지를 사용하여 노이즈를 제거한다.
또 그렇다면 Depth값을 정확하게 알고 있다면, SLAM을 사용하지 않아도 되는가? 그건 아니다. SLAM의 목적은 mapping도 있지만, localization도 필요하고, 맵을 확장시키는 기능도 있다.
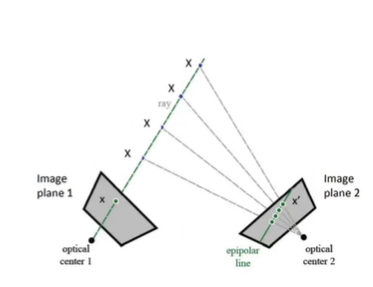
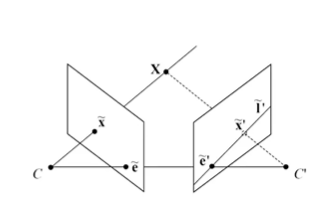
위의 이미지는 2장의 이미지를 사용하고 있는 모습이다. 바라보는 시점은 다르지만, 동일한 3D point를 바라보는 2개의 이미지가 있는 경우, 이를 2-view geometry라고 한다. monocular camera의 경우 1개는 previous image, 나머지 1개는 현재 image라 볼 수 있다. stereo camera인 경우에는 동시간대 왼쪽 오른쪽 카메라에 대한 이미지라 생각할 수 있다.
이런 2-view geometry를 다른 말로 epipolar geometry라고도 한다. image plane 1에서의 3D point-> 2D point로의 mapping을 할 때의 projection line이 있고, 이는 위의 그림에서 초록색 선에 해당한다. 이제부터는 초록색 선을 ray라 부르고자 한다. Visual SLAM을 수행할 때, 3D point가 2D image point로 projection될 때의 직선을 ray라고 한다. 이 ray를 image plane2에서도 바라볼 수 있을 것이다. ray를 image plane2에 투영되는 것을 재투영이라 한다. image plane2안에 그려진 ray를 투영한 직선을 epipolar line이라 한다. image plane1과 image plane2가 함께 바라보는 3D point는 무조건 epipolar line위에 존재한다.
image plane1과 image plane2의 rotation과 translatino을 정확하게 구하기 위해서는 image plane1에 존재하는 x와 image plane2에 존재하는 x’의 연관성이 반드시 필요하다.
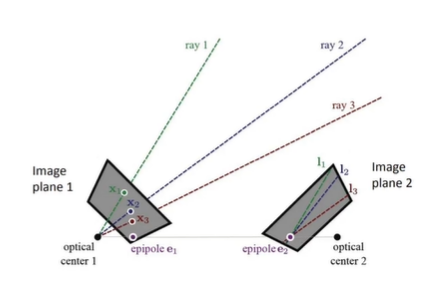
이번에는 2-view에서 image plane1이 3개의 3D point를 바라보고 있다고 생각해보자. 각각의 point들마다의 ray1,2,3이 존재할 것이고, image plane2에 재투영하면 3개의 epipolar line이 존재한다. 이 3개의 line이 한 점에서 만날 때, 이 점을 epipole이라 한다. 이 점은 모든 ray가 시작되는 지점인 optical center이다. 간단하게 보면 점들이 3차원으로 뻗어나가고 있을 때, 이 ray들은 한 점에서 만나고, 이를 image plane2에서 바라보고 있으니 epipolar line이 만나는 점은 당연히 ray들이 교차하는 지점인 optical center이다.
즉, epipole은 반대편 이미지의 optical center가 투영된 것이다. 지난 카메라의 위치가 보이는 것이거나 stereo 일 경우에는 옆의 카메라를 바라보고 있다고 생각할 수 있다.
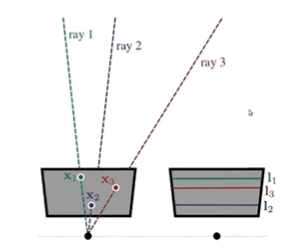
만약 카메라가 같은 방향을 바라보고 있다면, 위와 같은 상황이 발생할 것이고, 이 때는 epipole이 존재하지 않고, 따라서 ray1,2,3은 모두 평행하다. stereo 카메라의 경우 calibration과정을 거치고 나서 rectification이라는 과정을 수행한다. 이는 카메라의 위치들을 조정해서 모두 같은 방향을 바라보도록 만드는 과정이다.
이러한 과정을 수행하는 이유는 그림에서 힌트가 있다. 이러한 경우 모든 epipolar line들이 가로로 선이 그어지게 되고, 그렇게 되면 두 이미지의 연관성을 찾고 싶으면 x1,x2,x3 각각의 row를 찾으면 된다. x1에 대한 correspondence를 찾고 싶으면 l1을 탐색하고, x2에 대한 correspondence를 찾고 싶으면 l2를 탐색하면 된다.
대각선의 선에서부터 correspondence를 찾는 것은 오래걸리고 메모리도 많이 차지할 것이다. 그러나 가로선의 경우에는 픽셀의 정보도 붙어있어서 쉽게 매칭을 해줄 수 있다.

monocular 카메라에 대해 로봇이나 자동차가 직진을 하고 있다면, 위의 그림과 같은 상황이 발생한다. 이 경우에는 epipole1과 epipole2가 직선에 놓이게 된다. 즉 이미지 상에서의 동일한 위치에 형성될 것이고, epipolar line은 방사 형태가 될 것이다. 이 경우는 굳이 어렵게 correspondence를 구하지 않아도 rotation이 없다는 것을 알 수 있고, translation값만 알면 곧바로 이동거리를 판단할 수 있다.
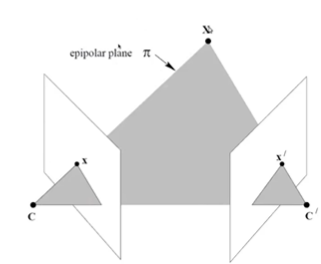
다시 epipolar geometry로 돌아와서 좌측 이미지와 우측 이미지의 optical center들과 3D point를 연결하면 삼각형이 만들어진다. 이 삼각형을 epipolar plane이라 한다. 이 plane은 epipolar line과 epipole의 정보를 모두 가지고 있다. 그리고 좌측 이미지의 optical center와 우측 이미지의 optical center를 연결하는 직선을 baseline이라 한다. 이 직선은 두 카메라 간의 거리값을 표현한다. baseline이 길면 길수록 삼각측량의 정확도가 커지기도 한다.

baseline이 이미지 plane을 통과하면 통과하는 점이 epipole을 이룬다. 즉 epipole들은 baseline 직선 위에 올라가 있다는 것을 알 수 있다. 이미지를 통해 수많은 3D point를 관찰할 수 있다. 3D point, x를 위아래로 움직여보면 그에 맞게 epipolar plane이 생기는데, 이들은 baseline을 중점으로 회전을 한다는 것을 확인할 수 있다. 존재할 수 있는 epipolar plane은 굉장히 많을텐데, 이 모든 가능성을 epipolar pencil이라 한다.
이 모든 특징들을 조합해서 correspondence가 존재하기 위한 조건들을 3가지로 요약할 수 있다.
- 3D point,
x는 epipolar plane위에 있어야 한다. - 모든 epipolar line들은 epipole과 교차해야 한다.
- 모든 baseline은 epipole과 교차해야 하며 epipolar plane은 baseline을 반드시 포함하고 있어야 한다.
이러한 조건들을 기하학적 표현으로 geometry constraints라 한다. 어떤 현상이 나타나기 위해서 존재해야 하는 조건들을 의미한다.
Essential / Fundamental matrix
essential matrix와 fundamental matrix는 VSLAM에서 epipolar geometry가 사용되는 개념이다.
e-matrix(essential matrix)는 epipolar constraint에 대한 정보를 담고 있는 3x3 matrix이다. 카메라 간의 모션을 추정하기 위해서는 correspondence를 정확하게 아는 것이 중요하다. 이 correspondence를 정확하게 얻어낼 수 있도록 하는 것이 epipolar constraint이기 때문에, 이 e-matrix를 얻어내는 것이 굉장히 중요하다. epipolar constraint가 뜻하는 것은 결국 두 카메라간의 회전과 이동을 담고 있다.
$ E = t * R $
$ \widetilde{x}^T E \widetilde{x} = 0 $
E는 essential matrix이고, 이는 2개의 2d point를 이어주는 역할을 한다. t는 3x1 matrix translation, R는 3x3 matrix의 rotation을 뜻하고, 이 둘은 벡터곱 연산을 수행한다. 벡터곱 연산을 수행하기 위해서는 차원이 같아야 하므로 3x1 translation matrix를 대칭행렬(https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=sw4r&logNo=221357931060) 형태로 바꿔주어 3x3 matrix로 변환시킨다. 결국 essential matrix는 3x3 matrix로 구성될 것이고, 이를 SVD를 통해 t와 R로 분해한다.
그러나 이 essential matrix를 그대로 사용하려면 한가지 오류가 있다. 이 x가 어떻게 표현되어 있는지 모른다는 것이다. essential matrix를 표현할 때는 image point, x는 normalized image plane에서의 점으로 표현한다. 그러나 실제 이미지를 다루고자 할 때는 픽셀로서 좌표를 표현해야 하기에 normalized된 좌표를 픽셀 좌표로 변환해줘야 한다. 이 과정에 필요한 matrix가 instrinsic matrix인거고, instrinsic matrix까지 결합하여 matrix를 표현한 것을 Fundamental matrix라 한다. Fundamental matrix, F는 intrinsic matrix, K에 대해 다음과 같이 표현된다.
$ F = (k’^{-1})^T E K^{-1} $
$ F = (K’^{-1})^T [t_x] R K^{-1} $
$ \widetilde{x}’^T F \widetilde{x} = 0 $
이 때, $ [t_x] $ 는 translation matrix를 대칭행렬한 형태를 의미하고, k’,k는 stereo camera의 경우 두 이미지 plane은 각각의 intrinsic matrix를 가지기 때문에, 분리하여 표현해주었다. -1는 inverse를 의미한다.
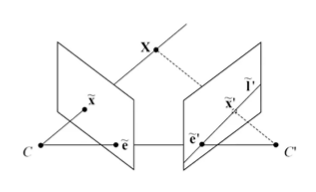
이 fundamental matrix를 사용하여 좌측 이미지의 점 $ \widetilde{x} $와 F-matrix를 곱하면 우측 이미지에서의 epipolar line, l'이 된다.
$ l’ = F\widetilde{x} $
그리고, 아까 봤던 식을 통해 새로운관계식을 구상할 수 있다.
$ \widetilde{x}’^T F \widetilde{x} = 0 $
$ \widetilde{x}’^T l’ = 0 $
즉, 우측 이미지의 좌표와 우측 이미지에서의 epipolar line과 곱해주면 0이 된다. line과 point가 교차한다면 0이 된다는 정의가 그대로 적용된다. 이를 통해 correspondence를 굉장히 빠르게 구할 수 있다. 우측 이미지에서의 픽셀이 왼쪽이미지에서는 어떤 픽셀과 correspondence를 이루는가에 대한 문제를 풀기 위해 좌측 이미지에서 모든 픽셀에 가능성을 둘 필요없이 우측 이미지에서의 좌표와 F-matrix를 곱해줘서 나오는 line과 벡터 연산을 해서 0이 나오는 픽셀만 사용하면 되는 것이다.
Essential matrix와 Fundamental matrix를 구하는 방법은 각각 5-point algorithm, 8-point algorithm이 있다. 최소 5개, 8개의 correspondence가 존재할 때 Essential matrix, Fundamental matrix를 구할 수 있다.

Fundamental matrix의 경우 7DoF를 가지고 있다. translation(tx,ty,tz), totation(rx,ry,rz), focal length(f)와 c(principal point)가 있는데, 여기서 scale 값을 구할 수 없기 때문에 1개를 빼서 7이 된다. essential matrix는 5DoF, translation 3, rotation 3에서 1이 빠져서 5가 된다.
DoF(degree of freedom)를 알아야 이 값을 추론하기 위해서 가져야 하는 최소한의 데이터의 수가 어떤지 알 수 있고, 아무런 prior없이 값을 추론하기 위해서는 데이터가 요구하는 DoF의 수만큼의 데이터가 필요하기 때문에 DoF를 알고 있어야 한다. 이처럼 최소한의 데이터의 수로 문제를 해결하는 알고리즘을 minimum-solver라 한다. 5DoF의 essensial matrix를 추론하기 위해서는 5개의 데이터가 필요하므로 이는 minimum-solver에 해당하지만, 7DoF의 fundamental matrix를 추론하기 위해서는 8개의 데이터가 필요하므로 이는 non-minimum-solver에 해당한다.
fundamental matrix를 추론하기 위해 7개의 데이터를 사용해도 되지만, 오류를 잡기도 어렵고, 내부 구조가 어려워져서 대체로 8개로 추론하도록 한다.
essential matrix나 fundamental matrix를 구하는 방법은 OpenCV에 잘 구현되어 있다. essential matrix의 경우는 recoverPose(), fundamental matrix의 경우는 findFundamentalMat()이다.
구현 과정
- 2장의 다른 이미지에 대해 feature matching을 한다.
- 이를 기반으로 fundamental matrix를 구해서 카메라들 간의 모션 값을 추정한다.
- 한 장의 이미지에 F-matrix를 곱하면 다른 한장의 이미지에서의 epipolar line이 나온다.
- 원래 이미지에서의 픽셀값과 line을 벡터 연산하여 0이 되는 지점을 예측한다.
그러나 이 때, 문제는 f-matrix를 구하고 나서 점을 예측하고 나서야 feature matching이 잘 되었는지 아닌지를 판단할 수 있다.
Outlier rejection(removal)
SLAM에서 inlier와 outlier가 있다. inlier는 관측 시 예상했던 데이터 분포에 포함되어 있는 데이터이고, outlier는 데이터 분포에서 벗어나 있는 데이터를 말한다. 데이터 분포에서부터 얼마나 떨어져있는지에 대한 에러로 판단하는데, 모든 데이터는 노이즈를 가지고 있기 때문에 에러값으로만 판단하기는 어렵다. 그래서 inlier를 기대하면서 맞는 값, outlier를 기대하지 않았으면서 틀린 값이라 정의하고자 한다.
outlier가 나타나는 이유는 밝기 정보가 급격하거나, 회전, 블러, 가림 등의 깔끔한 이미지를 얻지 못하거나 기존의 기하학적 정보가 깨지기 때문일 것이다. outlier를 filtering해야 더 정확하고 좋은 알고리즘이 된다.
컴퓨터 비전에서는 2가지의 outlier filtering 알고리즘이 있다.
- closed-form algorithm
- 여기에는 수많은 minimum solver 알고리즘이 있다. fundamental matrix를 구하는 8-point는 정확하게 매칭이 된 correspondence를 전제로 한다. 이중에 하나라도 정확하지 않으면 잘못된 결과가 나온다.
- iterative optimization
- 훨씬 더 많은 데이터로 동작하지만, 이 데이터들이 좋은 데이터라고 판단이 될 때까지 지속적으로 찾아가는 알고리즘이다.
- 데이터 분포 속 inlier 사이에서 패턴을 찾아서 필터링을 한다. 그 데이터를 따르지 않는 데이터가 들어올 경우 잘못된 예측이 발생할 수 있다.
outlier를 제거하여 깔끔한 inlier데이터들만 남겨놓고 계산을 하게 만드는 것이 중요하다. 그에 대한 예시를 몇가지 살펴보자.
Linear regression
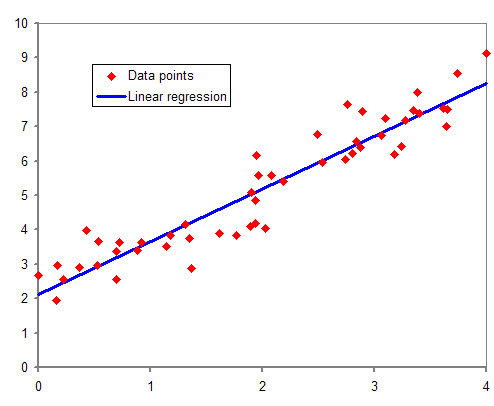
2D plot에서 여러 개의 데이터 포인트들을 가로지르는 가장 정확한 직선을 추정하는 알고리즘이다. 이 때, 직선에 대해 각각의 데이터 포인트들마다의 거리값(error)를 가지므로 이에 대해 절대값을 취하는 SAE, 또는 제곱을 취하는 SSE가 있다. 이 error를 줄이는 것을 목표로 한다.
이는 너무 한계가 뚜렷해서 최근에는 다양한 알고리즘들이 개발되었다.
- RANSAC
- M-Estimator
- MAXCON
이 중 가장 유명한 RANSAC에 대해 알아보고자 한다.
RANSAC
RANSAC(RAndom SAmple Consensus)은 1981년에 개발된 기법이다. 무작위로 데이터 샘플을 뽑아 모델을 만들고, 모델에 대해 데이터의 적합성을 판단한다. RANSAC은 template으로 안에서 돌아가는 알고리즘은 따로 지정해야 한다.
RANSAC 기법 과정
- 무작위로 최소한의 데이터를 뽑는다.
- 데이터를 기반으로 모델을 추정한다.
- 추론한 모델을 기반으로 score를 측정한다. - 현재까지의 가장 최고의 score보다 현재의 score가 들어오면 score를 업데이트한다.
- 다시 1번으로 돌아간다.
쉽게 보기 위해 homography에 RANSAC알고리즘을 추가한 과정을 설명하면 다음과 같다.
- homography를 구하기 위해 필요한 최소한의 데이터는 4개이므로 무작위로 4개의 데이터를 뽑는다.
- 그 데이터를 기반으로 homography matrix를 추정한다.
- reprojection(재투영) error를 계산한다.
- 한 이미지 픽셀값들에 homography matrix를 곱하면, 다른 하나의 이미지에 대한 픽셀값들이 나오게 된다.
- 이 때, GT와 계산값과의 error를 전부 더한다. 이 때, 특정 error threshold를 설정해서 그 error보다 낮은 값만 추가되도록 할 수 있다.
- 최고 score(lowest error)보다 현재의 score(error)가 낮으면 score를 업데이트한다.
- 1번으로 되돌아간다.
최적의 모델을 얻기 위해 반복해야 할 횟수(T)를 논문에서 함께 제시했다.
$ T = \cfrac{log(1-p}{log(1-(1-e)^s)} $
- T : 최적의 모델을 얻기 위해 반복해야 할 횟수
- P : 뽑은 모델이 전부 inlier로 이루어지길 바라는 확률 (want P% accuracy)
- e : 전체 데이터셋 중 inlier와 outlier의 비율 (the dataset in made of e% inliers and (1-e)% outliers)
- s : 매 loop마다 뽑아야 하는 샘플의 수 (minimal sample of data to be a minimal set)
이 때, 구한 T를 통해 전체 프로세스의 시간을 대략적으로 짐작할 수 있다. T에 homography solver 프로세스 한 번 돌리는데 걸리는 시간을 곱해서 전체 프로세스 시간을 구할 수 있다.
RANSAC의 장점
- outlier를 제거할 수 있다.
- T를 통해 총 걸리는 시간을 구할 수 있다.
- 운좋게 더 빠르게 찾는다면 더 빨리 끝낼 수 있다.
- 굉장히 쉬워서 이해하기 쉽다.
RANSAC의 단점
- 알고리즘 자체가 랜덤성을 가지고 있으므로 돌릴 때마다 결과값이 다르게 나온다. 이로 인해 모델의 성능이 좋아지고 있는지 랜덤성으로 좋아진건지 판단하기 어렵다.
- 전체 데이터셋에 inlier보다 outlier의 수가 더 많아질 경우 실행 시간이 급격하게 늘어난다.
- 만약 RANSAC 알고리즘이 실패하면 모든 가능성을 순회하도록 속도로 수렴하게 된다.
- 하나의 데이터셋에서 여러 모델을 돌릴 수 없다. 예를 들어 RANSAC을 통해 동시에 3개의 Fundamental matrix를 구할 수가 없다.
Modern RANSACs
기존의 RANSAC을 보안한 Modern RANSAC도 있다. 기존의 RANSAC에는 여러가지 단점이 존재했다. 동시에 다중 모델을 추론하는 것이 불가능했다. 또한, 무작위로 뽑기 때문에, prior 정보를 활용하지 못했고, 센서에는 노이즈가 많은 편인데 기존의 RANSAC은 노이즈가 거의 없는 알고리즘으로 구현되어 있었다.
개량 RANSAC에는 종류가 엄청 많다. 그래서 어떤 것을 써야할지 고민이 되기도 하는데, 가장 좋은 방법은 모든 방식을 공부해서 자신의 태스크에 맞게 사용하는 것이다. 또는 여러 방식을 조합할수도 있다. 여러 가지의 방식들을 간략하게 소개하려고 한다.
Early-stop method
좋은 모델을 빨리 찾는 경우 RANSAC 사이클을 끝내는 방식이다. 원래의 사이클보다 빨리 끝나면 해당 시간이 비게 되므로 뒤에 프로세스를 땡겨서 처리할수도 있다.
이 방식을 구현하기 위해서는 3가지 변수를 미리 정의해야 한다.
- minimum iteration : 최소한의 퀄리티를 보장하기 위한 최소한의 반복 수
- maximum iteration : 좋은 모델이 안찾아지면 계속 반복하는 것이 아닌 반드시 최대 특정 반복 수만큼 돌고 끝내도록 함
- success score : 특정 score보다 높게되면 반복을 멈추도록 하기 위함
PROSAC
PROSAC은 이미지 매칭에 특화된 RANSAC기법으로 데이터의 prior를 잘 활용하는 기법이다. PROSAC은 descriptor matching을 할 때, L2 norm이나 Hamming distance로 측정하게 되는데, descriptor들 간의 distance가 작을수록 모델 추론을 할 때 더욱 정확하게 추론할 가능성이 높다. 그래서 PROSAC은 낮은 distance를 가진 descriptor match를 샘플링하도록 만들었다.
PROSAC의 장점은 운이 나빠서 완전 실패하더라도, 기존의 RANSAC으로 수렴하기에 반드시 기존의 RANSAC보다 성능이 좋다는 것이다.
PROSAC 동작 방식
- 2개의 이미지에 대해 descriptor matching을 수행한다. 이 과정에서 match마다의 descriptor간의 distance를 기록한다.
- distance를 오름차순으로 정렬한다.
- 몇개씩 탐색할지에 대한 size(n)을 지정해준다.
- distance 리스트에서 n개의 top data를 샘플링한다.
- 샘플링한 데이터들로 모델을 추론한다.
- 좋은 결과가 나오면 score값을 업데이트하고, 원래의 score보다 낮으면 n을 증가시킨다.
- 다시 4번으로 돌아간다.
PROSAC은 5~10개의 loop만으로 최적의 모델을 찾는 경우가 많다.
Lo-RANSAC
Lo-RANSAC은 데이터셋의 데이터 패턴을 활용한 방법이다. 보통 inlier는 뭉쳐있고, outlier는 산개한 특징이 있어서 그것을 활용했다. 즉, inlier데이터를 활용해서 분포를 찾고나면 정답은 그 근처에 있으므로 랜덤한 위치로 이동할 필요가 없다.
Lo-RANSAC에서는 RANSAC 사이클 안에 추가로 RANSAC을 넣어 더 정확한 값을 찾는다.
Lo-RANSAC 동작 방식
- 최소한의 데이터를 샘플링
- 모델을 추론한다.
- 기존의 score보다 현재의 score가 안좋다면 다시 1번으로 돌아간다.
- best score보다 좋은 score가 들어왔다면, inner RANSAC을 실행하여 방금 전 모델 score를 평가할 때 inlier라고 판단했던 데이터들을 새로운 데이터로 사용하여 데이터를 샘플링한다.
- 샘플링된 데이터로 모델을 추론한다.
- 만약 best score보다 현재 score가 높다면 score를 업데이트한다.
- 만약 best score보다 낮다면 2-1로 돌아간다.
- maximum loop를 초과하면 inner RANSAC loop를 빠져나간다.
- 기존의 score보다 현재의 score가 안좋다면 다시 1번으로 돌아간다.
- Gauss-Newton method나 Levenberg-Marquardt method 와 같은 최적화 기법을 수행한다. 이 때도, best score를 갱신한다.
- 1번으로 다시 돌아간다.
descriptor match score(distance)를 가지고 있다면 PROSAC을 사용하는 것이 좋지만, 없다면 Lo-RANSAC을 사용하는 것이 적합하다. PROSAC을 사용하더라도inner-RANSAC을 함께 조합해서 사용하면 더욱 좋은 성능을 낼 수 있다.
