CS231N chapter 9 - CNN Architectures

8강 리뷰

1) Tensorflow

2) Pytorch

3) static Vs dynamic graph

CNN Architecture

크게 AlexNet, VGGNet, GoogLeNet, ResNet 등이 있다.

LeNet

LeNet은 산업에 성공적으로 적용된 최초의 ConvNet이다.

이미지를 입력으로 받아 stride = 1인 5x5 필터를 거치고 몇 개의 conv Layer과 pooling layer를 거친다. 끝단에 FC layer가 붙는다.

간단한 모델이지만, 엄청난 성공을 거둔 모델이다.

AlexNet

2012년에 AlexNet이 나왔다. 최초의 Large scale CNN이다. ImageNet을 아주 잘 수행했다.

LeNet와 유사하나 layer 수가 더 많아졌다.

AlexNet의 전체 layer이다.

AlexNet(
  (features): Sequential(
    (0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))
    (1): ReLU(inplace=True)
    (2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (4): ReLU(inplace=True)
    (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (7): ReLU(inplace=True)
    (8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (9): ReLU(inplace=True)
    (10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU(inplace=True)
    (12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
  (classifier): Sequential(
    (0): Dropout(p=0.5, inplace=False)
    (1): Linear(in_features=9216, out_features=4096, bias=True)
    (2): ReLU(inplace=True)
    (3): Dropout(p=0.5, inplace=False)
    (4): Linear(in_features=4096, out_features=4096, bias=True)
    (5): ReLU(inplace=True)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)

기본적으로 conv- pool - normalization이 2번 반복되고, conv layer가 조금 더 붙고 (conv 3,4,5…), 그 뒤에 pooling layer(Maxpooling)가 있다. 마지막에는 FC layer가 몇 개 붙어있다.

따라서, 5개의 conv layer과 3개의 FC layer로 구성되어 있다.

기본적으로 imageNet으로 학습시킨 모델이므로 입력 크기는 227x227x3이다.

(0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))

첫 레이어인 conv1은 96개의 stride = 4인 11x11 필터가 존재한다. 그렇다면 출력은 (227-11)/4 + 1 = 55 x 55 x 96의 activiation map이 생성된다.

또한, 입력 depth(channel)는 3이다. 따라서 첫번째 layer는 11x11x3 필터가 96개 있으므로, (11x11x3)x96 개의 파라미터를 가지고 있다.

(2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)

두번째 layer는 pooling layer이다.

여기에는 stride = 2 인 3x3 필터가 있다. 따라서 이 레이어의 출력의 크기는 27x27x96이다. pooling layer은 depth가 변하지 않는다.

pooling layer에는 파라미터가 존재하지 않으므로 0개다. 파라미터는 우리가 학습시키는 가중치다. conv layer에는 학습할 수 있는 가중치가 있지만, pooling layer는 학습시킬 파라미터가 존재하지 않는다.

모든 레이어의 파라미터 사이즈와 갯수를 계산해보자.

• INPUT : [227 x 227 x 3]
• CONV1 : 96개의 11x11 filter at stride 4, padding 0 -> (227 - 11)/4 + 1 = 55 -> [55 x 55 x 96], p = (11x11x3)x96
• MAX POOL1 : 3x3 filters at stride 2 -> (55 - 3)/2 + 1 = 27 -> [27 x 27 x 96], p=0
• NORM1 : [27 x 27 x 96]
• CONV2 : 256 5x5 filters at stride 1, pad 2 -> (27 + 2*2 - 5)/1 + 1 = 27 -> [27 x 27 x 256], p=(5x5x96)x256
• MAX POOL2 : 3x3 filters at stride 2 -> (27 - 3)/2 + 1 = 13 -> [13 x 13 x 256], p=0
• NORM2 : [13 x 13 x 256]
• CONV3 : 384 3x3 filters at stride 1, pad 1 -> (13 + 2*1 - 3)/1 + 1 -> 13 -> [13 x 13 x 384], p=(3x3x256)x384
• CONV4 : 384 3x3 filters at stride 1, pad 1 -> (13 + 2*1 - 3)/1 + 1 -> 13 -> [13 x 13 x 384], p=(3x3x384)x384
• CONV5 : 256 3x3 filters at stride 1, pad 1 -> (13 + 2*1 - 3)/1 + 1 -> 13 -> [13 x 13 x 256], p=(3x3x384)x256
• MAX POOL3 : 3x3 filters at stride 2 -> (13 -3)/2 + 1 = 6 -> [6 x 6 x 256], p=0
• FC1 : p=4096
• FC2 : p=4096
• FC3 : p=1000

사실 이것은 summary 함수를 통해 확인해볼 수 있다.

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1           [-1, 64, 56, 56]          23,296
              ReLU-2           [-1, 64, 56, 56]               0
         MaxPool2d-3           [-1, 64, 27, 27]               0
            Conv2d-4          [-1, 192, 27, 27]         307,392
              ReLU-5          [-1, 192, 27, 27]               0
         MaxPool2d-6          [-1, 192, 13, 13]               0
            Conv2d-7          [-1, 384, 13, 13]         663,936
              ReLU-8          [-1, 384, 13, 13]               0
            Conv2d-9          [-1, 256, 13, 13]         884,992
             ReLU-10          [-1, 256, 13, 13]               0
           Conv2d-11          [-1, 256, 13, 13]         590,080
             ReLU-12          [-1, 256, 13, 13]               0
        MaxPool2d-13            [-1, 256, 6, 6]               0
AdaptiveAvgPool2d-14            [-1, 256, 6, 6]               0
          Dropout-15                 [-1, 9216]               0
           Linear-16                 [-1, 4096]      37,752,832
             ReLU-17                 [-1, 4096]               0
          Dropout-18                 [-1, 4096]               0
           Linear-19                 [-1, 4096]      16,781,312
             ReLU-20                 [-1, 4096]               0
           Linear-21                 [-1, 1000]       4,097,000
================================================================
Total params: 61,100,840
Trainable params: 61,100,840
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.59
Forward/backward pass size (MB): 8.49
Params size (MB): 233.08
Estimated Total Size (MB): 242.16

구조를 자세히보면 모델 끝에는 3개의 FC layer가 있다. 2개의 fc layer은 4096 node를 가지고, 마지막 layer은 FC layer은 softmax를 통과하여 1000개의 imageNet 클래스를 분류한다.

ReLU, dropout을 사용하였고, batch size는 128이다. optimization으로는 SGD momentum을 사용했다. 초기의 lr은 1e-2이었다가 val accuracy가 올라가지 않는 지점에서는 학습이 종료되는 시점까지 1e-10까지 줄였다. weight decay를 사용했고, 마지막에는 모델 앙상블로 성능을 향상시켰다.

이 당시에는 Batch Normalization이 존재하지 않았기 때문에, flip, jitter, colo norm 등의 data augmentation을 많이 사용했다.

다른 Network와의 차이점이라 하면 모델이 두개로 나뉘어져 서로 교차한다는 점이다. 그 당시의 GPU의 메모리가 3GB뿐이었기에, 분산시켜 넣은 것이다. 즉, 각 GPU에의 Depth는 48이다.

conv1,2,4,5 는 같은 gpu내에 있는 feature map만 사용하기 때문에 각 gpu는 48개의 feature map만 사용한다.

그러나 conv3, FC6,7,8 은 이전 계층의 전체 feature map과 연결되어 있다. 이 layer 들은 gpu간의 통신을 하기 떄문에 전체 depth를 전부 가져올 수 있는 것이다.

alexnet은 2012년 image classification benchmark에서 우승한 모델이다. 최초의 CNN 기반 우승 모델이고, CNN을 보편화시킨 모델이라 볼 수 있다.

ZFNet

ZFNet은 2013년 imageNet challange에서 우승한 모델이다.

alexnet과 레이어 수가 같고, 기본적인 구조가 같다. stride size, 필터 수 와 같은 하이퍼파라미터를 조절하여 개선한 모델이다.

VGGNet

2014년에는 엄청난 변화가 있었다. architecture도 변하고, 성능도 훨씬 향상되었다. 가장큰 차이점은 네트워크가 훨씬 깊어진 것이다. 이전의 8개 layer에서 19개의 layer와 22개의 layer로 늘어났다.

2014년의 우승 모델은 GoogLeNet이고 VGGNet이 2등이었다. 하지만, 다른 트랙에서 VGGNet이 1위를 차지했다.

VGG(
  (features): Sequential(
    (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU(inplace=True)
    (2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (3): ReLU(inplace=True)
    (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (6): ReLU(inplace=True)
    (7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (8): ReLU(inplace=True)
    (9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU(inplace=True)
    (12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (13): ReLU(inplace=True)
    (14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (15): ReLU(inplace=True)
    (16): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (17): ReLU(inplace=True)
    (18): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (19): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (20): ReLU(inplace=True)
    (21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (22): ReLU(inplace=True)
    (23): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (24): ReLU(inplace=True)
    (25): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (26): ReLU(inplace=True)
    (27): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (29): ReLU(inplace=True)
    (30): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (31): ReLU(inplace=True)
    (32): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (33): ReLU(inplace=True)
    (34): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (35): ReLU(inplace=True)
    (36): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(7, 7))
  (classifier): Sequential(
    (0): Linear(in_features=25088, out_features=4096, bias=True)
    (1): ReLU(inplace=True)
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU(inplace=True)
    (5): Dropout(p=0.5, inplace=False)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)

우선 VGGNet을 살펴보자면, 네트워크가 훨씬 더 깊어졌고, 더 작은 필터를 사용했다. 16~19개의 layer을 사용하고, 3x3필터만 사용했다. 주기적으로 pooling을 수행하였다. vggnet은 아주 간단하면서도 고급진 아키텍처이다.

3x3 필터를 사용한 이유는 필터가 작으면 파라미터의 수가 작아진다. 따라서 큰 필터에 비해 layer를 조금 더 많이 쌓을 수 있다. 즉, depth를 더 키울 수 있는 것이다.

그렇다면, stride = 1인 3x3 필터를 3 개 쌓을 때의 receptive field는 어떻게 될까?

receptive field는 필터가 한번에 볼 수 있는 입력의 영역을 의미한다.

첫번째 layer의 receptive field는 3x3이다. 두번째 layer의 경우 첫번째의 layer 출력의 3x3만큼 보고, 3x3중 각 사이드는 한 픽셀씩 더 볼 수 있다. 따라서 두번째 layer는 실제로 5x5 receptive field를 가진다. 세번째 layer는 두번째 layer의 3x3을 보게 되므로 입력 layer의 7x7을 보게 된다.

따라서, 3x3 필터를 3개 쌓는 것은 하나의 7x7 필터를 사용하는 것과 같다. ?????????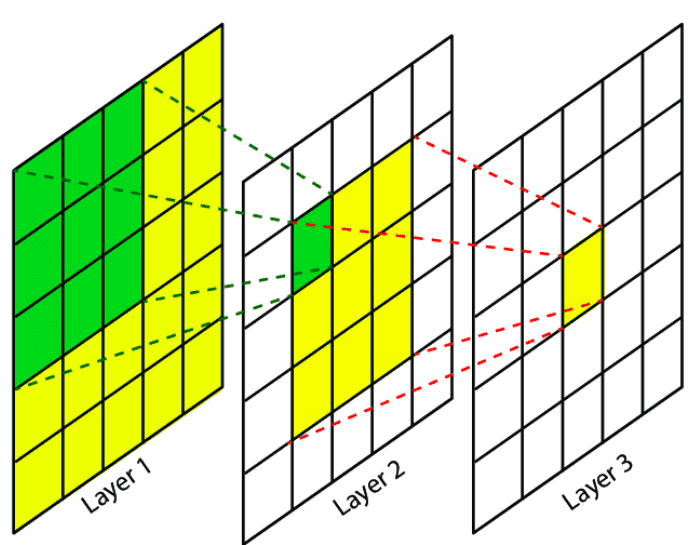

실질적인 receptive field를 동일하게 가지면서 파라미터 개수를 줄일 수 있고, non-linearity를 늘릴 수 있기 때문에 3x3 필터가 이점을 가질 수 있는 것이다.

• 3x3 필터의 파라미터 수는 depth가 3이라는 가정하에, (filter 크기) x feature map depth = (3X3X3) X 3 = 81, 3개를 쌓아야 하므로 81x3 = 243
• 7x7 의 경우 7x7x3x3x1 = 441

따라서 3x3필터를 3개 쓰는 것이 7x7 필터 1개 쓰는 것보다 개수가 적다.

전체 구조와 파라미터 수는 다음과 같다.

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1         [-1, 64, 227, 227]           1,792
              ReLU-2         [-1, 64, 227, 227]               0
            Conv2d-3         [-1, 64, 227, 227]          36,928
              ReLU-4         [-1, 64, 227, 227]               0
         MaxPool2d-5         [-1, 64, 113, 113]               0
            Conv2d-6        [-1, 128, 113, 113]          73,856
              ReLU-7        [-1, 128, 113, 113]               0
            Conv2d-8        [-1, 128, 113, 113]         147,584
              ReLU-9        [-1, 128, 113, 113]               0
        MaxPool2d-10          [-1, 128, 56, 56]               0
           Conv2d-11          [-1, 256, 56, 56]         295,168
             ReLU-12          [-1, 256, 56, 56]               0
           Conv2d-13          [-1, 256, 56, 56]         590,080
             ReLU-14          [-1, 256, 56, 56]               0
           Conv2d-15          [-1, 256, 56, 56]         590,080
             ReLU-16          [-1, 256, 56, 56]               0
           Conv2d-17          [-1, 256, 56, 56]         590,080
             ReLU-18          [-1, 256, 56, 56]               0
        MaxPool2d-19          [-1, 256, 28, 28]               0
           Conv2d-20          [-1, 512, 28, 28]       1,180,160
             ReLU-21          [-1, 512, 28, 28]               0
           Conv2d-22          [-1, 512, 28, 28]       2,359,808
             ReLU-23          [-1, 512, 28, 28]               0
           Conv2d-24          [-1, 512, 28, 28]       2,359,808
             ReLU-25          [-1, 512, 28, 28]               0
           Conv2d-26          [-1, 512, 28, 28]       2,359,808
             ReLU-27          [-1, 512, 28, 28]               0
        MaxPool2d-28          [-1, 512, 14, 14]               0
           Conv2d-29          [-1, 512, 14, 14]       2,359,808
             ReLU-30          [-1, 512, 14, 14]               0
           Conv2d-31          [-1, 512, 14, 14]       2,359,808
             ReLU-32          [-1, 512, 14, 14]               0
           Conv2d-33          [-1, 512, 14, 14]       2,359,808
             ReLU-34          [-1, 512, 14, 14]               0
           Conv2d-35          [-1, 512, 14, 14]       2,359,808
             ReLU-36          [-1, 512, 14, 14]               0
        MaxPool2d-37            [-1, 512, 7, 7]               0
AdaptiveAvgPool2d-38            [-1, 512, 7, 7]               0
           Linear-39                 [-1, 4096]     102,764,544
             ReLU-40                 [-1, 4096]               0
          Dropout-41                 [-1, 4096]               0
           Linear-42                 [-1, 4096]      16,781,312
             ReLU-43                 [-1, 4096]               0
          Dropout-44                 [-1, 4096]               0
           Linear-45                 [-1, 1000]       4,097,000
================================================================
Total params: 143,667,240
Trainable params: 143,667,240
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.59
Forward/backward pass size (MB): 242.32
Params size (MB): 548.05
Estimated Total Size (MB): 790.96
----------------------------------------------------------------

VGG19를 불러왔다. forward/backward pass 시 필요한 메모리양이 242MB로 다른 아키텍처에 비해 많은 편이다.

전체 파라미터의 경우 alexnet보다 훨씬 많다. 가장 많은 파라미터를 사용하는 layer는 FC layer이다. FC layer가 fully connected(dense connection)되었기 때문이다. 최근 네트워크의 경우 파라미터를 줄이기 위해 FC layer를 없애기도 한다.

동일하게 활성함수로 relu를 사용하고, fc layer에서 dropout을 사용했다.

Q. 네트워크가 깊어질수록 layer의 필터 개수를 늘려야 하는가?(channel depth를 늘려야 하는지) => 필수는 아니지만 depth를 늘리는 경우가 많은데, 계산량을 일정하게 유지시키기 위해서다. downsampling을 하면 Width와 Height가 작아져서 depth를 늘려도 부담이 적어진다.

모델 성능을 향상시키기 위해 앙상블 기법을 사용했다.

layer를 보면 conv3-64 라는 것이 있는데, 이는 64개 필터를 가진 3x3 conv 필터라는 뜻이다.

마지막 FC7은 1000 class를 분류하기 위한 layer로 아주 좋은 feature represetation(특징 표현)을 가지고 있다. 다른 task에서도 능력이 뛰어나기에 vgg가 많이 사용된다.

GoogLeNet

GoogLeNet(
  (conv1): BasicConv2d(
    (conv): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
    (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
  )
  (maxpool1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=True)
  (conv2): BasicConv2d(
    (conv): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
    (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
  )
  (conv3): BasicConv2d(
    (conv): Conv2d(64, 192, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn): BatchNorm2d(192, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
  )
  (maxpool2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=True)
  (inception3a): Inception(
    (branch1): BasicConv2d(
      (conv): Conv2d(192, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
    )
    (branch2): Sequential(
      (0): BasicConv2d(
        (conv): Conv2d(192, 96, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(96, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicConv2d(
        (conv): Conv2d(96, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn): BatchNorm2d(128, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (branch3): Sequential(
      (0): BasicConv2d(
        (conv): Conv2d(192, 16, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(16, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicConv2d(
        (conv): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn): BatchNorm2d(32, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (branch4): Sequential(
      (0): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=True)
      (1): BasicConv2d(
        (conv): Conv2d(192, 32, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(32, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
  )
  (inception3b): Inception(
    (branch1): BasicConv2d(
      (conv): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn): BatchNorm2d(128, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
    )
    (branch2): Sequential(
      (0): BasicConv2d(
        (conv): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(128, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicConv2d(
        (conv): Conv2d(128, 192, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn): BatchNorm2d(192, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (branch3): Sequential(
      (0): BasicConv2d(
        (conv): Conv2d(256, 32, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(32, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicConv2d(
        (conv): Conv2d(32, 96, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn): BatchNorm2d(96, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (branch4): Sequential(
      (0): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=True)
      (1): BasicConv2d(
        (conv): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
  )

GoogLeNet은 총 22개의 layer을 가지고 있다.

GoogLeNet에서 가장 중요한 것은 효율적인 계산에 관한 그들만의 특별한 관점이 있고, 높은 계산량을 아주 효율적으로 수행하도록 네트워크가 디자인되어 있다.

GoogLeNet은 inception module을 여러 개 쌓아져 있다. 그리고 FC layer가 없다. 파라미터를 줄이기 위해서이다. 전체 파라미터가 6M 정도이다. 60M인 alexNet보다 훨씬 적은 양이다. 그럼에도 더욱 깊다.

Inception module

구글은 좋은 로컬 네트워크 typology를 디자인하고자 했고, network-in-network라는 개념으로 이를 구현했다.

여기서 local network를 inceptino module이라 한다. 내부에는 동일한 입력을 받는 다양한 필터가 병렬로 존재하고, 이 layer의 입력을 받아서 다양한 conv 연산을 수행한다.

중간의 그림을 보면 1x1, 3x3, 5x5 conv에 3x3 pooling도 있다. 각 layer에서 각각의 출력 값이 나오는데, 이 출력은 모두 depth방향으로 합쳐진다.(concatenate) 이런 방식으로 합치면 하나의 tensor로 출력이 결정되고, 이 하나의 출력을 다음 layer로 전달하는 것이다.

지금까지는 다양한 연산을 수행하고 이를 하나로 합쳐준다는 단순한 방식(naive way)를 살펴보았다.

• naive way의 문제점

계산 비용이 크다.

128개의 1x1 필터, 192개의 3x3필터, 96개의 5x5 필터가 있다고 하자. 그리고 입력 크기는 28x28x256이라고 하자.

stride를 조절하여 입/출력 간의 spatial dimension(receptive field)를 유지시킨다.

이 경우 1x1 conv필터 하나당 28x28 feature map을 생성하게 되기 때문에, 1x1x128 conv의 출력은 28x28x128이 된다. 1x1 conv의 경우 입력 depth가 256이므로 동일하게 256인데, 128개의 필터 하나당 28x28 feature map을 생성하게 된다.

똑같이 3x3x192 conv를 하면 28x28x192 가, 5x5x96 conv를 하면 28x28x96이 출력될 것이다.

conv는 입력 depth인 256만 가지고 내적을 한다고 볼 수 있기 때문이다.

즉, conv는 (입력 데이터 크기 W x H) x (filter 개수) 의 출력값을 가진다.

이 때, spatial dimention을 유지하기 위해 zero padding한다.

3x3 pooling layer의 경우 입력 그대로 28x28x256으로 나온다.

이를 다 합치면 28x28x(128+192+96+256) = 28x28x672 의 출력값이 된다. 결론적으로 dimention은 변하지 않았지만, depth가 엄청나게 커졌다.

1x1 conv에서의 전체 연산량은 28x28x128x256으로 엄청 많다. 3x3/5x5 도 마찬가지일 것이다. 특히 pooling layer에서는 더더욱 많다. 총 연산을 합치면 850M 정도가 된다.

레이어를 거칠수록 점점 더 늘어나게 된다. 이 문제를 해결하기 위해서 bottleneck layer를 이용한다.

bottleneck layer는 conv연산을 시작하기 전 입력을 더 낮은 차원으로 보내는 방법이다.

1x1 conv를 살펴보자. 1x1 conv는 내적을 수행한다. 그러면서 filter 개수를 활용해 depth만 줄일 수 있다. 입력의 depth를 더 낮은 차원으로 만드는 것이다.

이를 input feature map들 간의 선형결합(linear combination) 이라고 하기도 한다.

따라서, 3x3/5x5 conv 이전에 1x1 conv 64개를 추가한다. 또, pooling layer 이후에도 1x1 conv를 추가한다.

1x1 conv를 bottleneck layer의 역할로 추가되는 것이다.

이전과 비교했을 때,

• 1x1 conv 64 => 28x28x64x1x1x256
• 1x1 conv 64 => 28x28x64x1x1x256
• 1x1 conv 128 => 28x28x128x1x1x256
• 3x3 conv 192 => 28x28x192x3x3x64
• 5x5 conv 96 => 28x28x96x5x5x64
• 1x1 conv 64 => 28x28x64x1x1x256 => total 350M « 850M

전과 확연히 차이나게 줄어들었다.

자세하게 보자면, 입력은 28x28x256이고, 3x3 conv 앞쪽의 1x1 conv 출력은 28x28x64이다.

따라서 28x28x64로 전의 28x28x256보다 줄었다.

정리하면, 1x1 conv를 추가함으로써 계산량을 조절할 수 있다

1x1 conv를 추가한다고 해서 데이터 변형이 일어나지 않는다.

GoogLeNet의 앞단(초기 6개 layer)에는 일반적인 네트워크 구조다. 이때는 conv-pool를 반복한다.

이후 inception module을 쌓는데, 모두 조금씩 다르다. 그리고 마지막에는 classifier 결과를 출력한다.

아래 부분을 보면 추가적으로 줄기가 뻗어져 있다. 이들은 보조분류기(auxiliary classifier)이다. 이것들은 작은 미니 네트워크다. average pooling과 1x1 conv가 있고 FC layer도 몇개 붙고, softmax로 1000개의 imageNet class를 구분한다.

이 부분에서도 loss를 계산한다. 네트워크 끝에서 뿐만 아니라 이 두곳에서도 계산하는 이유는 네트워크가 꽤 깊기 때문이다.

보조분류기를 중간 layer에 달아주면 추가적인 gradient를 얻을 수 있고, 중간 layer의 학습도 도울 수 있다.

googleNet 학습 시 보조 분류기에서 나온 loss의 모든 합의 평균을 계산한다.

또, 보조분류기에서 추가적인 gradient를 얻는 이유는 네트워크가 엄청 깊은 경우 gradient 신호가 점점 작아지게 되고 결국 0에 가깝게 된다. 그래서 보조분류기를 이용해서 추가적인 gradient 신호를 추가한다.

ResNet

resnet은 152개의 layer를 가진 엄청나게 깊은 네트워크다. ResNet은 residual connections 라는 방식을 사용한다.

맨 처음 생각한 방법은 conv-pool layer을 계속해서 깊게 쌓으면 성능이 좋아질까 라는 것이었다.

하지만 성능은 좋이지지 않았다.

네트워크가 깊어지게 되면 어떤 일이 발생할까?

• 20 layer Vs 56 layers

기본적으로 네트워크가 깊어지면 파라미터가 엄청 많아지기 때문에 overfit이 발생할 것이다. overfit이 발생하면 test error는 높더라도, training error는 아주 낮아야 정상이다.

하지만 56 layer을 보면 training error가 20 layer보다 안좋다.

따라서 더 깊은 모델임에도 test 성능이 낮은 이유는 overfitting 문제가 아니라는 것을 알 수 있다.

여기서 ResNet 저자들은 더 깊은 모델 학습 시 최적화(optimization) 가 더 어려워진다는 가설을 세웠다.

모델이 더 깊다면 적어도 더 얕은 모델만큼은 성능이 나와야 정상아닌가 생각할 것이다.

그래서 해결책으로 일단 더 얕은 모델의 가중치를 깊은 모델의 일부 레이어에 복사했다. 나머지 레이어는 identity mapping을 했다. identity mapping이란 input을 output으로 내보내는 것을 말한다.

이와 같이 얕은 모델을 복사해왔기 때문에, 비슷한 성능이 나올 수 있다.

이 방식을 녹여 모델을 만들고자 했다.

ResNet의 아이디어는 단순히 layer를 쌓는 방법(direct mapping)이 아니라 residual mapping의 방법이었다.

레이어가 직접 H(x)를 학습하기보다 이와 같이 H(x) - x를 학습할 수 있도록 만들어준다. 이를 위해 skip connection를 도입한다.

오른쪽 고리 모양을 보면, skip connection은 가중치가 없으며 입력을 indentity mapping을 통해 그대로 출력단으로 보낸다.

실제 레이어는 변화량(delta)만 학습하면 된다. 입력 x에 대한 잔차(residual)이라 할 수 있다.

즉, 원래의 출력인 H(x) 대신 입력 x를 그대로 가져와 H(x)와 x의 차이(변화량)인 F(x)만을 학습시킨다.

그래서, 최종 출력 값은 input X + 변화량(residual) 이다.

이 방법을 사용하면 학습이 더 쉬워진다. 가령 input = output 인 상황이라면 F(x)(residual) = 0 이므로 모든 가중치를 0 으로 만들어주면 된다.

네트워크는 residual만 학습하면 되기 때문에 한층 더 쉬워졌다. 전체 full mapping을 학습하는 대신, residual mapping 만 학습하는 것이고, 출력 값도 결국엔 입력 x와 가까운 값이기 때문이다.

이때, layer의 출력과 skip connection의 출력은 같은 차원이다. 같지 않더라도 depth-wise padding으로 차원을 맞춰줄 수 있다.

사실 이것들은 ResNet 저자의 가설이었기에, 입증된 바는 없다. 그러나 실제로 ResNet을 사용할 때 성능이 더 좋아지기도 한다.

전체 ResNet 구조를 나타낸 것이다. 아래는 직접 resnet을 불러온 결과를 가져와봤다.

하나의 residual blocks는 두개의 3x3 conv layer로 이루어져 있다. 이렇게 구성해야 잘 동작한다. 이 Residual block을 아주 깊게 쌓는다.

또한, 주기적으로 필터를 두배씩 늘리고, stride 2를 이용하여 downsampling한다.

그리고 맨 처음에 7x7 conv-64를 붙였고, 네트워크 끝에는 FC layer가 없다. 그 대신 global average pooling layer를 사용한다. 맨 마지막에 존재하는 FC 1000 은 클래스 분류를 위한 노드이다.

GAP(global average pooling layer)는 하나의 map 전체를 average pooling 하는 것을 말한다.

ResNet 중에서도 가장 많이 사용되고 있는 모델은 resnet101 이다. 101은 모델의 depth(layer)를 말한다. 101말고도 34, 50 100, 152 등이 있다.

depth가 50이상일 때 1x1 conv를 도입하여 depth를 줄이는 bottleneck layer를 도입한다. 이는 GoogLeNet에서 사용한 방법과 유사하다.

bottleneck layer을 통해 3x3 conv의 계산량을 줄인다. 그리고 뒤에 다시 1x1 conv를 추가하여 depth를 다시 원래대로 늘린다.

정리하자면

• 모든 conv layer 다음에 batch norm 을 사용한다.
• 초기화로는 Xavier을 사용하는데, 추가적으로 scaling factor(2로 나눔)를 더 수행한다. 이 방법은 SGD + momentum 에서 좋은 초기화 성능을 보인다.
• learning rate는 validation error가 줄어들지 않는 시점에서 조금씩 줄여주며 조절한다.
• minibatch size = 256
• weight dacay 사용, 1e-5
• dropout 사용 x

ResNet의 top-5 error은 3.6%로 인간의 성능(5%)보다 뛰어나다고 한다.

아래는 ResNet 아키텍처를 직접 가져와봤다.

''' ResNet101 structure '''
ResNet(
  (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (relu): ReLU(inplace=True)
  (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  (layer1): Sequential(
    (0): Bottleneck(
      (conv1): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (downsample): Sequential(
        (0): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): Bottleneck(
      (conv1): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
    )
    (2): Bottleneck(
      (conv1): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
    )
  )
  (layer2): Sequential(
    (0): Bottleneck(
      (conv1): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (downsample): Sequential(
        (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): Bottleneck(
      (conv1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
    )
    (2): Bottleneck(
      (conv1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
    )
    (3): Bottleneck(
      (conv1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
    )
  )

ResNet과 관련된 최근 연구들

• Identity Mapping in Deep Residual Networks

이 논문에서는 ResNet의 블록 디자인을 향상시켰다. 그 방법으로 ResNet block path를 조절했다.

새로운 구조는 direct path 간격을 늘려서 정보들이 앞으로 더욱 더 잘 전달되고 backprop도 더 잘 될 수 있도록 한 것이다.

• Wide Residual Networks

기존의 ResNet 논문은 깊게 쌓는 것에 집중했지만, 사실 중요한 것은 depth가 아니라 residual이라 주장한 논문이다.

residual connection이 있다면 네트워크가 굳이 더 깊게 필요가 없다고 주장한다.

그래서 깊이 대신 residual block을 더 넓게 만들었다. 즉, conv layer의 필터를 더 많이 추가한 것이다.

원래 F개의 filter가 존재했다면 여기서는 F * k개의 필터를 사용한다.

그렇게 하여 50 layer만 있어도 152 layer의 resnet보다 성능이 좋다는 것을 입증했다.

이 방법의 또 다른 이점은 계산 효율이 증가한 것이다. 왜냐하면 병렬화가 더 잘되기 때문이다.

네트워크의 depth를 늘리는 것은 sequential의 증가, 즉 위아래로 늘어나는 것이라면, conv 필터를 늘리는 것은 width가 넓어지는 것이다.

• ResNeXt

ResNet의 저자의 논문으로 residual block의 width를 계속 연구한다. filter 수를 늘리는 것이다. 각 redisual block 내에 다중 병렬 경로를 추가한다. 이들은 pathway(경로)의 총 합을 cardinality(관계수)라고 불렀다.

하나의 bottleneck ResNet block은 비교적 작지만 이런 얇은 block들이 병렬로 여러 개를 묶었다.

layer를 병렬로 묶는다는 것에서 inception module과도 연관이 있다.

• Stochastic Depth

이 논문의 주제는 depth이다. 네트워크가 깊어질수록 vanishing gradient가 발생한다. 뒤로 전달될수록 점점 grdient가 작아진다.

그래서 train time에서 layer의 일부를 제거하여 short network를 만들어 training 능력을 약간 향상시키는 것이다.

그 방법으로 일부 네트워크를 골라 identity connection으로 만들어버린다. dropout과 유사하다고 볼 수 있다. 동일하게 test time에서는 full layer를 사용한다.

이제 좀 다른 아키텍처들을 살펴보고자 한다.

Other Network architecture

• Network in Network (NiN)

기본 아이디어는 MLP conv layer이다. 네트워크 안에 작은 네트워크를 삽입하는 것이다. 각 conv layer 안에 (MLP(Multi-layer perceptron) = FC layer)을 쌓는다.

단순히 conv filter만 사용하지 않고, 좀더 복잡한 계층을 만들어서 feature map을 얻어보자는 아이디어다.

NIN은 기본적으로 FC layer을 사용한다. 이를 1x1 conv layer라고도 한다.

GoogLeNet이나 ResNet보다 먼저 bottleneck 개념을 정립했다.

• FractalNet

이 논문에서는 residual connection이 필요없다고 주장한다. 그래서 FractalNet에서는 residual connection이 전혀 없다.

그들은 오른쪽 그림과 같이 fractal(차원분열도형)한 모습이다.

FactalNet에서는 shallow(얕은)/deep 경로를 출력에 모두 연결한다. 다양한 경로가 존재하지만 train time에는 dropout과 같이 일부 경로만을 이용해서 train한다.

• DenseNet

densely connected convolutional network, 즉 빼곡하게 연결된 convolutional network 이다.

dense block을 사용하는데, 한 layer가 그 layer 하위의 모든 layer와 연결된다. 네트워크의 입력 이미지가 모든 layer의 입력으로 들어가는 것이다. 그 모든 layer의 출력이 각 layer의 출력과 concat(합침)된다.

이 dense block을 통해 vanishing gradient 문제를 완화시킬 수 있다고 주장한다.

그리고 dense connection은 feature을 더 잘 전달하고 더 잘 사용할 수 있게 해준다고 한다. 각 layer의 출력을 다른 layer에서도 여러번 사용하기 때문이다.

• SqueezeNet

여기서는 fire module이라는 것을 도입했다. squeeze layer는 1x1 filter들로 구성되고, 출력 값이 1x1,3x3 filter들로 구성되는 expand layer의 입력이 된다. squeezeNet은 AlexNet 과 비슷한 accuracy를 보이지만 파라미터는 50배 더 적다.

Comparing Model Complexity

지금까지 배운 모델이거나 조금 변형된 모델들이다.

incetion을 보면 V2,V3 등이 있는데 가장 좋은 모델은 당연히 V4이다. v4는 resnet + inception 모델이다.

오른쪽 그래프를 보면 계산 복잡성이 추가하여 볼 수 있다. y축은 top-1 accuracy로 높을수록 좋다. x축은 연산량으로 오른쪽일수록 연산량이 많다. 원의 크기는 메모리 사용량이다.

초록색 원은 VGGNet이다. 가장 효율성이 작다. 메모리는 크면서 계산량이 많다. 성능은 나쁘지 않다.

파란색 원은 GoogLeNet인데, 가장 효율적인 네트워크다. 거의 왼쪽에 있으며 메모리 사용량도 작다.

초기 AlexNet 모델은 accuracy가 낮다. 계산량은 작지만, 메모리 사용량이 비효율적이다.

ResNet의 경우 적당한 효율성을 가지고 있다. 메모리 사용량과 계산량은 중간이지만, accuracy가 최상위에 있다.

왼쪽 그래프틑 forward pass 시간이다. 단위는 ms인데, VGG가 제일 오래걸린다. 200ms, 즉 초당 5정도 처리한다.

오른쪽은 전력소모량인데, 이는 논문을 참고하길 바란다.

https://arxiv.org/abs/1605.07678

Reference

• http://cs231n.stanford.edu/2017/syllabus.html
• https://velog.io/@guide333/%ED%92%80%EC%9E%8E%EC%8A%A4%EC%BF%A8-CS231n-9%EA%B0%95-Training-Neural-Networks-Part-2-2
• https://velog.io/@cha-suyeon/CS231n-Lecture-9-%EA%B0%95%EC%9D%98-%EC%9A%94%EC%95%BD