CS231N chapter 3 - Loss function and Optimizations

• 2강 리뷰

1) image deformation

2) 그를 해결하기 위한 data-driven approach

3) Nearest Neighbor method, K-Nearest Neighbor(KNN)

4) cross validation

5) hyperparameter

6) linear classifier

linear classifier은 parametric classifier의 한 종류다. parametric classifier란 training data의 정보가 parameter인 행렬 W로 요약된다는 것을 뜻한다.

linear classifier은 이미지를 입력받으면 하나의 긴 벡터로 편다. 데이터를 고차원 공간에서의 일종의 decision boundary를 학습시킨다는 것으로 볼 수 있다.

Loss Function

위의 사진은 linear classifier을 적용한 classification이다. 정답 class가 가장 높은 score를 가져야 좋은 classifier인데, 위의 숫자를 보았을 때, 정답 class가 그렇게 높은 score를 가지지 못한다. 따라서 이는 좋지 못한 classifier이다.

score를 높이기 위해서는, 가중치 W를 어떻게 만들고, 가장 좋은 W를 어떻게 구하는지 알아야 한다.

w를 입력받아 각 score를 확인하고, 이 w가 얼마나 괜찮은지를 정량화시켜주는 것이 손실함수, loss function이다.

이 loss function을 통해 가장 최적의 hyperparameter를 추정하는 것이 바로 최적화 과정, optimization이다.

train data에서 이미지에 해당하는 x와 레이블에 해당하는 y가 있고, 보통 x는 알고리즘의 input에 해당된다.

이때, test의 x를 통해 y를 예측하고 정답과 비교하게 된다.

Loss, L은 :

• Li : 손실함수
• f(xi,W) : 내가 classifier를 사용해서 나온 class의 score
• yi : 실제 class의 정답 값 ( 고양이의 3.2 )
• N : class 의 수

최종적인 L은 결국 각 N개 샘플들의 Loss 평균이다.

multi-class SVM loss

SVM도 마찬가지로 KOOC 강의 - 머신러닝학습개론 을 참고하면 좋다.

multi-class SVM(Support Vector Machine)은 여러 class를 다루기 위한 이진 SVM의 일반화 형태다.

이진 SVM이란 두 개의 class만 다룬다는 뜻이다. 각 데이터는 positive/negative로 분류된다.

SVM Loss Li 는 :

Li 공식은 정답 class의 score가 제일 높을 때만 실행한다.

Li을 구하기 위해서는 True인 카테고리를 제외한 나머지 카테고리 Y의 합을 구한다. 다시말해, 맞지 않는 카테고리를 전부 합친다는 것이다. 그리고 올바른 카테고리의 score와 올바르지 않은 카테고리의 score을 비교한다.

올바른 카테고리의 score가 올바르지 않은 카테고리의 score보다 높고, 그 격차가 일정 마진(safety margin)이상이라면, 전부 0으로 코딩시킨다. 여기서는 1이 마진에 해당한다.

Multi-class SVM 은 정답에 대한 score가 높을수록 loss function은 0에 가까워지고, 그 반대일수록 loss function은 계속 커진다. 이를 그래프의 모양을 따서 hinge loss(경첩) 이라고도 불린다.

위의 그림에서 Sj는 분류기의 output으로 나온 예측된 score다. 즉, j번째 class의 score인 것이다. yi는 이미지의 실제 정답 번호이다. x축은 Syi 정답 class의 score이고, y축은 Loss이다.

정답 카테고리의 점수가 올라갈수록 loss는 선형적으로 줄어들고, 이 로스는 0이 된 후에도 safety margin을 넘어설 때까지 무조건 더 줄어든다.

구하고자 하는 것은 정답 스코어가 다른 스코어들보다 높은지를 보는 것이다. 정답 score의 safety margin이 충분히 높지 않으면 Loss는 커지게 된다.

아래의 예시를 보자.

우선 정답이 아닌 클래스를 본다. cat이 정답 클래스이므로 car과 flog를 계산한다. 이때, cat 보다 car이 더 높으므로 loss는 발생한다.

정답 클래스는 cat 이고, 이것을 car과 비교할 경우 =>

sj = car score = 5.1, syi =cat score = 3.2


max(0,(Car score) 5.1 - (Cat score) 3.2 + 1(magin)) + max(0,(frog score) -1.7 - (Cat score) 3.2 + 1)
= max(0,2.9) + max(0, -3.9) 
= 2.9

따라서 SVM Loss = 2.9 가 된다.

이 2.9가 얼마나 분류기가 이 이미지를 잘 분류하는지에 대한 척도이다.

이 때, frog는 cat score 보다 훨씬 작으므로 loss가 0이라고 빠르게 구할 수도 있다.

또한, car로 loss를 구해본다 치면, car의 score가 frog나 cat과의 차가 1보다 크므로 loss는 0 이 된다.

frog도 구해보면 6.3+6.6 = 12.9 가 나온다.

이제 전체 training dataset에서 구한 loss들의 평균을 구하면 최종적인 loss를 구할 수 있다.

Q1. 만약 car score을 조금 변경시키면 loss에는 무슨 일이 일어나는가?

loss는 score 간에 상대적인 차이가 중요하기 때문에 큰 영향이 없다.

Q2. loss 값의 최솟값과 최댓값을 구하면 어떻게 되나?

모든 정답 클래스의 score가 제일 크면 모든 loss가 0이므로 최솟값은 0, 최댓값은 infinite

Q3. 초기 w가 0에 가까우면 모든 score 값은 0과 비슷해질 것이다. 이때 loss를 구하면?

class의 수 - 1 이다. loss를 계산할 때 정답이 아닌 클래스를 순회한다. 그러면 c-1개의 클래스를 순회하게 될텐데 비교하는 두 스코어가 비슷하니 margin 때문에 우리는 1 score을 얻게 된다.

• 이는 실제로 유용한 디버깅 전략이다. 처음 training을 시작할 때 loss가 (0-0+1)*(class num-1)= class-1이 아니라면 버그가 존재하는 것이다.

Q4. SVM Loss는 정답인 class는 빼고 다 더한다. 그렇다면 정답인 class도 더하게 된다면 어떻게 되는가?

일반적으로 우리가 정답만 제외하고 계산하는 이유는 loss가 0이 되야 하는데, 정답 class를 포함하게 되면 SVM Loos의 평균값이 1이 증가해지기 때문에 1이 가장 좋은 값이 된다.

Q5. Loss에서 전체합을 쓰는게 아니라 평균을 쓴다면?

어차피 class의 수는 정해져 있기에 scale이 작아지는 것 이외에는 별 차이없다.

Q6. 손실함수를 제곱을 취하게 되면 어떻게 되나?

값이 완전히 달라지게 된다.

Q7. W는 정답이 1개 뿐인가?

W는 test data에 적용할 때 가장 잘 성능이 측정되는 값을 고르는 것이기 때문에, 여러 개가 존재할 수 있다.

Regularization

training set에 model이 완전하게 fit하지 못하도록 복잡도를 개선하거나 차수를 낮추는 것을 말한다.

위의 그림과 같이 파랑 점들이 train data, 초록 점이 test data라 하고

파란 선은 train에서 fit한 decision boundary라 하고, 초록 선이 우리가 원하는 decision boundary라 하자.

train을 거쳐 나온 db는 원하던 db가 아니다. 따라서 test data를 입력할 시 성능이 좋지 않다. 이것을 overfitting이라고 한다.

이때, train dataset에 model이 완전하게 fit하지 못하도록 regularization term을 추가하여 모델이 좀 더 단순한 w를 선택하도록 도와준다.

오컴의 면도날과 같이 일반적으로 더 단순한 것을 선호하기 때문이다.

오컴의 면도날 : 단순성의 원리 혹은 절감의 원리로 불린다. 즉, 필요 이상의 고차원을 상정해서는 안된다는 것이다.

이렇게 되면 loss는 이제 data loss 와 regularzation loss 두 가지 항을 가지게 된다. 또, hyperparameter인 ⋋가 생긴다.

이 두 항은 trade-off 즉, 반비례하는 경향이 있다.

regularization의 두 가지 역할이 있는데, 하나는 모델이 더 복잡해지지 않도록 해주고, 두번째는 모델에 soft penalty를 추가하는 것이다.

이 soft penalty를 추가하면 계속 복잡한 모델을 사용하고 싶다면 이 penalty를 감수해야 한다. 라는 상황이 된다.

regularization에는 여러 종류가 있다.

• L1 regularization
  • L1 norm으로 w에 패널티를 부과
  • 행렬 w가 희소행렬이 된다.
  • 작은 가중치는 0으로 수렴 => 중요한 가중치만 남음
• L2 regularization
  • 보편적인 방법으로 weight decay라고도 불린다.
  • 가중치 w에 대한 euclidean norm 또는 squared norm 또는 1/2 * squared norm을 사용
  • w의 euclidean norm에 패널티를 부과
• Elastic net regularization
  • L1 과 L2를 섞은 방법
• Max norm regularization
  • L1, L2 대신 man norm을 사용

L2 regularization이 모델을 단순화시키는 과정은 아래와 같다.

1. train data인 x와 서로 다른 두 개의 w가 있다.
2. x는 4차원 벡터, w1=[1 0 0 0], w2=[0.25 0.25 0.25 0.25]
3. linear classification을 할 때 x와 w를 내적한다.
4. x와의 내적이 w1과 w2가 같기에 모델은 동일하다고 판단할 수 있지만, 더 단순한 모델을 선호해야 한다.
5. 이때, w1 보다 w2의 norm이 더 작기 때문에 w2를 더 선호하게 된다.

반면 L1의 경우 w1을 더 선호한다. L1은 복잡도를 다르게 정의한다. 가중치 w에 0의 갯수에 따라 모델의 복잡도를 판단한다.

L2의 경우 W의 요소가 전반적으로 퍼져있을 때 덜 복잡하다고 판단한다.

따라서 복잡도를 어떻게 정의하는지, 어떻게 측정하는지에 따라 다른 값이 나온다.

Softmax

Multinomial logistic regression 으로, 딥러닝에서 많이 사용된다.

SVM에서는 score 자체에 대한 해석은 고려하지 않았다. 어떤 분류 문제가 있고, 어떤 모델이 10개의 class에 대해 각 class에 해당하는 10개의 숫자를 출력할 때, multi-class SVM의 경우에는 그 스코어 자체는 크게 신경쓰지 않았다.

하지만 여기서의 손실함수는 score 자체에 추가적인 의미를 부여한다.

score에 지수를 취해서 양수가 되도록 만든다. 그 후 이 지수들의 합으로 다시 정규화시킨다.

이를 통해 확률 분포를 얻는다. 이것이 결국 해당 class일 확률을 의미하는 값이 될 것이다.

여기에 log를 취하는데, 손실 함수라는 것은 얼마나 잘되는지가 아니라 얼마나 잘 안되는지에 대해 측정하는 것이다. 따라서 (-)를 붙여야 한다.

식은 다음과 같다.

Li는 Loss, P는 확률 값이자 softmax function 이다. Sj는 예측한 class별 score이고, Syi는 해당 class의 정답 score이다.

정리하자면 score이 있으면 softmax를 거치고, 나온 확률 값에 -log를 한다.

Q1. Softmax loss의 최솟값과 최댓값은?

0~inf, 정답인 class의 확률은 1, 아닌 class의 확률은 0일 때 최솟값이 되므로, -log(1) = 0 이다. 그리고 만약 정답 class의 확률이 0이라면 -log(0) = inf 이다.

Q2. softmax loss에서의 디버깅은, 즉 score가 모두 0 근처에 모여있는 작은 수일 때 loss는?

-log(1/C)=log(C)가 된다.

SVM의 경우 일정 margin을 넘기기만 하면 더이상 성능 개선에 신경쓰지 않는다. 하지만 softmax는 지속적으로 성능을 높이려 한다.

Optimization

최적읜 w를 찾는 방법에는 무엇이 있는지 알아보자.

가장 간단하게 떠올릴 수 있는 방법은 Random search 이다. 임의로 샘플링한 w들을 엄청 모아 loss를 계산해 찾는다.

이방법은 너무 좋지 않은 방법이다.

그 다음으로 gradient descent 방식이 있다.

함수 값이 낮아지는 방향으로 독립 변수 값을 변형시켜가면서 최종적으로 최소 함수 값을 갖도록 하는 독립 변수 값을 찾는 방법이다.

loss의 gradient를 계산할 때, 미분 코드가 맞는지 확인하기 위해서 수치적 gradient를 사용한다.

Gradient Descent

while True:
    weights_grad = evaluate_gradient(loss_fun,data,weights)
    weights += step_size * weights_grad # perform parameter update

이 간단한 알고리즘은 우선 w를 임의의 값으로 초기화 한 후 loss와 gradient를 계산하고, 가충치를 gradient의 반대 방향으로 업데이트한다.

이것을 반복하다보면 결국에는 수렴하게 된다.

여기서 step_size는 하이퍼파라미터로 얼마나 나아갈지를 말해주는 것이다. 이는 learning rate라고도 한다. 트레이닝을 시작할 때 learning rate를 가장 먼저 체크하는 것이 좋다.

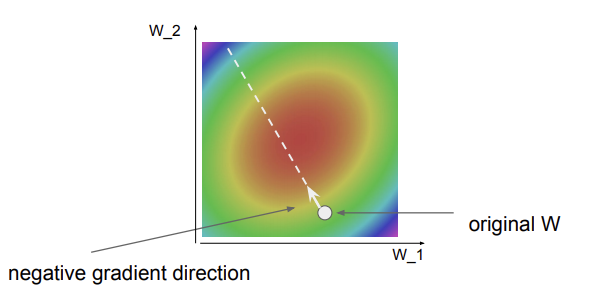
위의 그림은 손실함수에 대한 것으로 빨간 부분으 낮은 loss를 의미한다.

처음에는 임의의 w를 설정하고, 이를 -gradient를 계산하여 결국 가장 낮은 지점으로 도달할 것이다.

여기서 손실함수의 공식을 볼 때 전체 loss는 전체 training set의 loss의 평균이고, N이 엄청 커질 수도 있다.

그래서 Loss를 계산하는 것은 엄청 오래 걸리는 작업이다.

실제로는 더 단순하고 좋은 방법을 사용한다.

SGD

전체 데이터셋의 gradient와 loss를 계산하기보다 mini-batch를 활용하여 작은 training sample 집합으로 나눠서 학습한다.

이를 Stochastic Gradient Descent(SGD)라고 한다.

이는 SGD에 대한 식이다. minibatch는 일반적으로 32,64,128,256 등을 사용한다.

# minibatch gradient descent

while True:
    data_batch = sample_training_data(data,256) # 256단위로 minibatch
    weights_grad = evaluate_gradient(loss_fun,data_batch_weights)
    weights += step_size * weights_grad # perform parameter update

임의의 minibatch를 만들고, minibatch에서 loss와 gradient를 계산한다. 그리고 w를 업데이트한다.

추가적으로 이미지의 특징을 분석하는 방법을 조금 설명하고자 한다.

HOG

Histogram of oriented gradients는 NN이 유명해지기 전 이미지 특징을 분석하는 방법이다.

local orientation edges를 측정함으로써 픽셀안에서 가장 많이 존재하는 edge의 방향을 계산하고, edge direction을 양자화해서 양동이에 넣는다. 그 후 다양한 edge orienation에 대한 히스토그램을 계산한다.

즉, 각 edge의 방향에 해당하는 양동이가 존재하고, 픽셀마다 가장 많이 존재하는 방향에 해당되는 양동이에 그 픽셀을 집어넣는다.

그렇게 전체 특징 벡터는 각각의 모든 8x8 지역들이 가진 edge orientation에 대한 히스토그램이 되는 것이다.

visual words

bag of words라는 자연어처리에서 사용되는 아이디어에서 영감을 받았다.

어떤 문장이 있고 BOW에서 이 문장을 표현하는 방법은 문장의 여러 단어의 발생 빈도를 세서 특징 벡터로 사용한다.

이를 이미지에 적용하고자 한 것인데, 다양한 이미지를 nxn 픽셀로 나누고 그 조각들을 k-means와 같은 알고리즘으로 군집화한다.

군집화를 거치고나면, visual words는 픽셀의 다양한 색을 포착한다.

군집화한 것들로 새로운 이미지를 분석한다.

Reference

• http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture3.pdf
• https://cs231n.github.io/linear-classify/
• https://cs231n.github.io/optimization-1/
• https://cs231n.github.io/assignments2017/assignment1/