[데브코스] 10주차 - DeepLearning CNN

CNN을 들어가기 전에 DMLP에 대해 잠깐 살펴보고자 한다.

DMLP(Deep Multi Layer Perceptron)

딥러닝을 들어가기에 앞서 DMLP의 형태가 있다. 이는 다층 퍼셉트론보다 더 깊게 layer를 쌓은 것을 말하는데, 이는 완전 연결 구조를 가진다. 그에 따라 복잡도가 높아지고, 학습이 매우 느려진다. 또한 과잉적합(overfitting)이 발생할 수 있다.

그러나 CNN(convolutional neural network)의 경우 부분적으로 연결되어 있는 구조로 인해 격자 구조를 갖는 데이터에 적합하다.컨볼루션 연산을 통해 특징을 추출하고 영상 분류나 문자 인식 등 인식문제에서 높은 성능을 보인다.

Convolutional Neural Network

Convolution

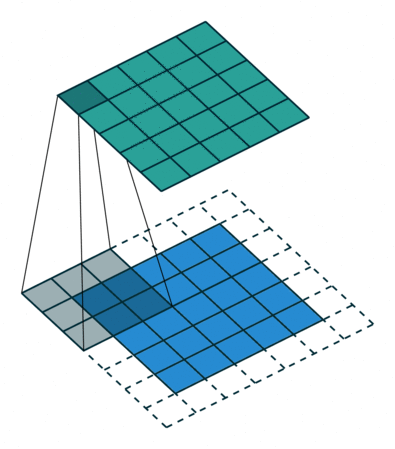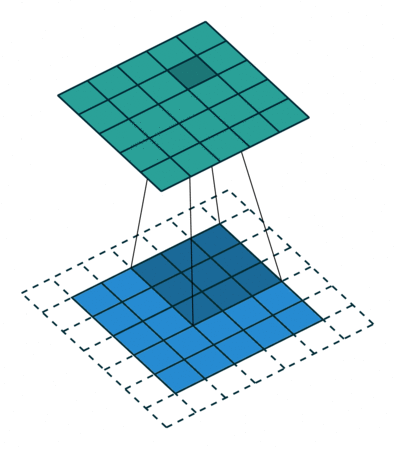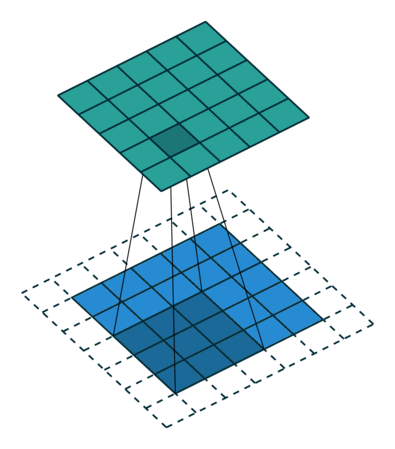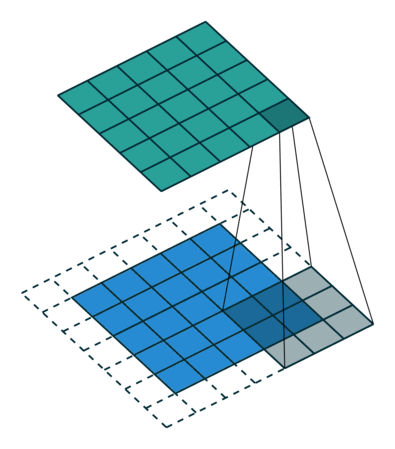
• padding : add zero in boundary of input image
• stride : elements of sliding window of convolution kernel

output shape

• output height : (input height - kernel height + padding size * 2) // stride + 1
• output width : (input width - kernel width + padding size * 2) // stride + 1

A * w = B의 연산의 경우

• A shape : [batch, input channel, input height, input width]
• w shape : [output channel ,input channel, kernel height, kernel width]
• B shape : [batch, output channel, output height ,output width]

연산량을 따질 때는 MAC(Multiply Accumulation Operation)단위를 사용한다.

convolution MAC : kw*kh*kc*oc*ow*oh*b(k:kernel, o:output, b:batch)

이 convolution은 sliding window 방식을 통해 연산을 수행하기 되고, 이를 for문으로 나타내면 다음과 같다.

for b in batch:
    for oh in output_height:
        for ow in output_width:
            for oc in output_channel:
                for kc in kernel_channel:
                    for kh in kernel_height:
                        for kw in kernel_width:

총 7번의 루프로 동작한다.

이는 너무 비효율적이기 때문에 IM2COL & GEMM 방식을 통해 더 간편한 연산 방식을 사용할 수 있다.

• IM2COL

n-dimension의 data를 2D matrix data로 변환시켜 더 효율적으로 연산한다.

data와 kernel을 2차원으로 변환하여 연산하면 2차원의 값이 출력될 것이다. 이를 다시 원래의 차원으로 변환하면 연산이 효율적으로 진행된다.

• kernel : [oc, kh*kw*ic]
• input : [kh*kw*ic, oh*ow]
• output : [oc, oh*ow]

이렇게 변환된 matrix를 연산하는 과정 자체를 GEMM(General Matrix to Matrix Multiplication)이라고 한다.

참고자료

CNN (numpy)

이 CNN의 연산을 pytorch나 tensorflow가 아닌 numpy만을 사용하여 구현해보고자 한다.

과정

1. sliding window convolution
2. IM2COL GEMM convolution

sliding window 방식

• function/convolution.py

import numpy as np

class Conv:
    # dilation : kernel이 얼마나 간격을 띄우고 연산할지에 대한 값
    def __init__(self, batch, in_c, out_c, in_h, in_w, k_h, k_w, dilation, stride, pad):
        self.batch = batch
        self.in_c = in_c
        self.out_c = out_c
        self.in_h = in_h
        self.in_w = in_w
        self.k_h = k_h
        self.k_w = k_w
        self.dilation = dilation
        self.stride = stride
        self.pad = pad

        self.out_h = (in_h - k_h + 2 * pad) // stride + 1
        self.out_w = (in_w - k_w + 2 * pad) // stride + 1

    def check_out(self, a, b):
        return a > -1 and a < b

    # naive convolution, sliding window matric
    def conv(self, A, B):
        # A * B = C
        # defice C size
        C = np.zeros((self.batch, self.out_c, self.out_h, self.out_w), dtype=np.float32)

        # 7 loop
        for b in range(self.batch):
            for oc in range(self.out_c):
                # each channel of output
                for oh in range(self.out_h):
                    for ow in range(self.out_w):
                        # each pixel of output shape
                        a_j = oh * self.stride - self.pad # a's y value == input's y value
                        for kh in range(self.k_h):
                            if self.check_out(a_j, self.in_h) == False: # a_j 가 in_h보다 크다면 연산 x
                                C[b, oc, oh, ow] += 0
                            else:
                                a_i = ow * self.stride - self.pad # a's x value == input's x value
                                for kw in range(self.k_w):
                                    if self.check_out(a_i, self.in_w) == False:
                                        C[b, oc, oh, ow] += 0
                                    else:
                                        C[b, oc, oh, ow] += np.dot(A[b, :, a_j, a_i], B[oc, :, kh, kw])
                                    a_i += self.stride # add x direction moving unit for kernel 
                            a_j += self.stride # add y direction moving unit for kernel
        return C

C는 결과를 저장하기 위한 저장소이다.

batch단위별로 결과 채널만큼 반복하고, 그것을 또 높이 단위로, 넓이 단위로 하나하나 루프를 돈다. 즉, [batch, out channel, out height, out width]의 형태만큼 순환을 해야 한다. output 결과를 계산해야 하는데, 계산을 위해 kernel크기만킄도 루프를 돌아야 한다. 반복을 하기 전에 입력의 row, col을 지정해주고, 예외 처리를 하여 연산에 오류가 나지 않는지 체크한다. 오류가 난다면 연산을 하지 않는다. row를 구할 때 kernel이 stride만큼씩 움직이므로 이를 곱한다. padding은 경계면에 0을 추가하여 중앙과 가장자리의 연산 수를 동일하게 맞춰주는 용도이다. 따라서 시작을 padding을 포함하여 시작할 수 있도록 (-)를 해준다.

• main.py

import numpy as np

from function.convolution import Conv

def convolution():
    print("convolution")

    # define the shape of input & weight
    in_w = 3
    in_h = 3
    in_c = 1
    out_c = 16
    batch = 1
    k_w = 3
    k_h = 3

    # define matrix
    x = np.arange(9, dtype=np.float32).reshape([batch, in_c, in_h, in_w])
    w = np.array(np.random.standard_normal([out_c, in_c, k_h, k_w]), dtype=np.float32)
    #print(x,"\n\n", w)

    Convolution = Conv(batch = batch,
                        in_c = in_c,
                        out_c = out_c,
                        in_h = in_h,
                        in_w = in_w,
                        k_h = k_h,
                        k_w = k_w,
                        dilation = 1,
                        stride = 1,
                        pad = 0)

    print("x shape : ", x.shape)
    print("w shape : ", w.shape)
    L1 = Convolution.conv(x,w)
    #print(L1)
    print("C shape : ", L1.shape) # batch, out_c, out_h, out_w

if __name__ == "__main__":
    convolution()

# ------------ # 

x shape :  (1, 1, 3, 3)  # batch, in_c, in_h, in_w
w shape :  (16, 1, 3, 3) # out_c, in_c, k_h, k_w
C shape :  (1, 16, 1, 1) # batch, out_c, out_h, out_w

im2col 방식

• function/convolution.py

    # IM2COL, change n-dim input to 2-dim matrix
    def im2col(self, A):

        # define output 
        mat = np.zeros((self.in_c * self.k_h * self.k_w, self.out_w * self.out_h), dtype=np.float32) 

        # matrix index
        mat_i = 0
        mat_j = 0

        # transform from A to mat
        for c in range(self.in_c):
            for kh in range(self.k_h):
                for kw in range(self.k_w):
                    in_j = kh * self.dilation - self.pad
                    for oh in range(self.out_h):
                        if not self.check_out(in_j, self.in_h):
                            for ow in range(self.out_w):
                                mat[mat_j, mat_i] = 0
                                mat_i += 1
                        else:
                            in_i = kw * self.dilation - self.pad
                            for ow in range(self.out_w):
                                if not self.check_out(in_i, self.in_w):
                                    mat[mat_j, mat_i] = 0
                                    mat_i += 1
                                else:
                                    mat[mat_j, mat_i] = A[0, c, in_j, in_i] # [batch, ic, ih, iw],   batch = 1이므로 0index
                                    mat_i += 1 # 1 x direction move
                                in_i += self.stride # move the stride unit as x axis
                        in_j += self.stride # move the stride unit as y axis
                    mat_i = 0 # initialization
                    mat_j += 1 # move next row at input

        return mat
    
    # gemm, 2D matrix multiplication
    def gemm(self, A, B):
        a_mat = self.im2col(A)
        b_mat = B.reshape(B.shape[0],-1) # kernel 4차원 텐서 차원을 reshape로 바꿀 수 있음, kernel은 [output channel ,input channel, kernel height, kernel width] 로 되어 있는데, 이를 [oc, kh*kw*ic]로 변환하기에
        c_mat = np.matmul(b_mat, a_mat)

        c = c_mat.reshape([self.batch, self.out_c, self.out_h, self.out_w])
        return c

이 때는 매번 루프를 돌 때마다 연산하는 것이 아닌 4d 차원을 2d로 변환한 후 연산을 진행한다. 따라서 변환해주기 위한 im2col을 먼저 선언한다.

• main.py

    L2 = Convolution.gemm(x,w)

    print(L2)
    print("L2 shape : ", L2.shape) # batch, out_c, out_h, out_w

pytorch와 위의 두 방식 시간 비교

# main.py
import time

    l1_time = time.time()
    for i in range(100):
        L1 = Convolution.conv(x,w)
    print("L1 time : ", time.time() - l1_time)


    l2_time = time.time()
    for i in range(100):
        L2 = Convolution.gemm(x,w)
    print("L2 time : ", time.time() - l2_time)


    # pytorch
    torch_conv = nn.Conv2d(in_c,
                            out_c,
                            kernel_size = k_h,
                            stride = 1,
                            padding = 0,
                            bias = False,
                            dtype = torch.float32)
    torch_conv.weight = torch.nn.Parameter(torch.tensor(w)) # 우리가 직접 생성한 weight를 집어넣음

    l3_time = time.time()
    for i in range(100):
        L3 = torch_conv(torch.tensor(x, requires_grad=False, dtype=torch.float32)) # x가 numpy로 생성되었기 때문에 tensor로 변환하여 실행
    print("L3 time : ", time.time() - l3_time)
    print(L3)

# ------------------- #

L1 time :  0.40502333641052246
L2 time :  0.017976760864257812
L3 time :  0.00850367546081543

L1 » L2 » L3 순으로 시간이 단축되는 것을 볼 수 있다.

CNN - pooling

pooling은 feature map의 크기를 줄이는 것을 말한다.

종류로는 max pooling / average pooling이 있다. max pooling의 작동 방식은 다음과 같다.

영역에서 최대값만 추출하므로 엣지부분을 많이 잡히게 출력된다.

그에 반해 average pooling의 경우 평균값을 사용하므로 스무딩한 형상을 띄게 된다.

pooling 직접 구현

• function/pool.py

import numpy as np

# 2d pooling
class Pool:
    def __init__(self, batch, in_c, out_c, in_h, in_w, kernel, dilation, stride, pad):
        self.batch = batch
        self.in_c = in_c
        self.out_c = out_c
        self.in_h = in_h
        self.in_w = in_w
        self.kernel = kernel
        self.dilation = dilation
        self.stride = stride
        self.pad = pad

        self.out_w = (in_w - kernel + 2 * pad) // stride + 1
        self.out_h = (in_h - kernel + 2 * pad) // stride + 1

    def maxpool(self, A):
        C = np.zeros([self.batch, self.out_c, self.out_h, self.out_w], dtype=np.float32)
        for b in range(self.batch):
            for c in range(self.in_c):
                for oh in range(self.out_h): # output 크기만큼 결과를 낼 것이므로
                    a_j = oh * self.stride - self.pad # 연산 시작 row
                    for ow in range(self.out_w):
                        a_i = ow * self.stride - self.pad # 연산 col
                        # kernel 크기만큼 중에서 가장 큰 값을 지정
                        C[b, c, oh, ow] = np.amax(A[:, c, a_j:a_j+self.kernel, a_i:a_i+self.kernel])
        return C

for문을 통해 하나하나 연산한다. amax라는 array안의 가장 큰 값을 추출해주는 메서드를 통해 2x2크기의 공간에서 최대값을 C array에 넣는다.

• main.py

# 간단한 forward 구조 생성
def forward_net():
    # define
    batch = 1
    in_c = 3
    in_w = 6
    in_h = 6
    k_h = 3
    k_w = 3
    out_c = 1

    x = np.arange(batch*in_c*in_w*in_h, dtype=np.float32).reshape([batch, in_c, in_w, in_h])
    w1 = np.array(np.random.standard_normal([out_c, in_c, k_h, k_w]), dtype=np.float32)

    Convolution = Conv(batch = batch,
                    in_c = in_c,
                    out_c = out_c,
                    in_h = in_h,
                    in_w = in_w,
                    k_h = k_h,
                    k_w = k_w,
                    dilation = 1,
                    stride = 1,
                    pad = 0)

    L1 = Convolution.gemm(x,w1)
    print("L1 shape", L1.shape) # L1 shape (1, 1, 4, 4)
    print("L1", L1)

    Pooling = Pool(batch = batch, # L1의 출력 Shape를 입력으로 넣어줘야 한다.
                    in_c = L1.shape[1],
                    out_c = L1.shape[0],
                    in_h = L1.shape[2],
                    in_w = L1.shape[3],
                    kernel = 2, # pooling의 커널 2x2
                    dilation = 1,
                    stride = 2,
                    pad = 0)

    L1_max = Pooling.maxpool(L1)

    print("\nL1 max shape : ", L1_max.shape)
    print("L1 max",L1_max)

# ---------------------- #

L1 shape (1, 1, 4, 4)
L1 [[[[484.84863 491.3175  497.78632 504.2552 ]
   [523.6616  530.1305  536.5993  543.0681 ]
   [562.47455 568.9434  575.4122  581.88104]
   [601.28754 607.75635 614.2252  620.694  ]]]]

L1 max shape :  (1, 1, 2, 2)
L1 max [[[[530.1305  543.0681 ]
   [607.75635 620.694  ]]]]

간단하게 forward과정만 보기 위해 함수를 선언해주었다. x를 input 형태로 만들어주고, w1을 생성해준다. 그 후 conv 이후에 pooling을 진행하므로 convolution을 먼저 진행해준다. conv는 gemm 함수를 사용했다. 이로 인해 출력되는 값은 (1,1,4,4) 형태로 리턴된다. 이를 pooling 해줄 때는 in_c, out_c 가 아닌 L1 conv 한 출력값 형태로 넣어줘야 한다.

당연히 input -> conv -> pooling -> output 순서로 진행되기 때문이다. 그렇게 maxpooling을 진행하면 [batch, in_c, in_h, in_w] -> [batch, out_c, (in_h - kernel + 2 * pad) // stride + 1,(in_w - kernel + 2 * pad) // stride + 1] 로 변환된다.

output : [1, 1, (4 - 2 + 2 * 0) // 2 + 1, (4 - 2 + 2 * 0) // 2 + 1] = [1,1,2,2]

CNN - FC layer

Fully Connected Layer로써 2d 특징맵을 1d 특징맵으로 변환한 후 fc weight와 연산하여 최종 결과를 출력하는 층이다.

이는 2d를 1d로 변환한 층이므로 연산랴이 엄청 크게 되고, 파라미터의 수가 이곳에 가장 많이 분포되어 있는 경우가 많다.

그래서 이를 해결하기 위해 1x1 convolutional layer로 바꿔서 만드는 모델도 많다.

fc layer 코드 구현

• funtion/fc.py

import numpy as np

class FC:
    def __init__(self, n_classes, in_c, out_c, in_h, in_w):
        self.n_classes = n_classes
        self.in_c = in_c
        self.out_c = out_c
        self.in_h = in_h
        self.in_w = in_w

    def fc(self, A, W):
        # A shape : [b,in_c, in_h, in_w] -> [b, in_c*in_h*in_w]
        a_mat = A.reshape([self.n_classes, -1])
        B = np.dot(a_mat, np.transpose(W, (1,0))) 
        return B

A, 입력의 shape은 [b,in_c, in_h, in_w] 이다. 이 4-dim 을 2-dim으로 변환한 후 fc layer 연산을 수행해야 하므로 [b, in_c*in_h*in_w]로 변환해준다.

B의 경우 출력값인데, vector 내적 연산을 수행하는 dot을 사용했고, w는 입력이 [1, in_c*in_h*in_w] 이므로 연산을 위해서는 순서를 바꿔줘야 한다. 그러므로 transpose 시켜준다.

• main.py

    # fully connected layer
    w2 = np.array(np.random.standard_normal([L1_max.shape[0], L1_max.shape[1]*L1_max.shape[2]*L1_max.shape[3]]), dtype=np.float32)
    Fc = FC(n_classes = L1_max.shape[0],
            in_c = L1_max.shape[1],
            out_c = 1, # 출력은 1채널이어야 함
            in_h = L1_max.shape[2],
            in_w = L1_max.shape[3])

    L2 = Fc.fc(L1_max, w2)

    print("L2 shape : ", L2.shape)
    print(L2)

# ------------------- #

L2 shape :  (1, 1)
[[1205.8112]]

이렇게 출력된 형태는 (1,1) == (n_classes, out_c) , 즉 각각의 클래스에 따른 확률값이다.

CNN - Activation

activation, 활성 함수는 비선형 함수로 sigmoid, tanh, ReLU, LeakyReLU 등이 있다.

sigmoid와 tanh는 역전파시 gradient vanishing 현상이 발생하므로 최근에는 사용하지 않는다. 또한, ReLU는 max 함수이므로 연산이 더 빠르기 때문에 ReLU를 많이 사용한다.

Activation 코드 구현

• function/activation.py

import numpy as np

# max(0,x)
def relu(x):
    x_shape = x.shape
    x = np.reshape(x, [-1]) # 몇 차원인지 모르기 때문에 1차원으로 변환
    x = [max(0,v) for v in x]
    x = np.reshape(x, x_shape)
    return x

def leaky_relu(x):
    x_shape = x.shape
    x = np.reshape(x, [-1])
    x = [max(0.1*v, v) for v in x]
    x = np.reshape(x, x_shape)
    return x
    
def sigmoid(x):
    x_shape = x.shape
    x = np.reshape(x, [-1])
    x = [ 1 / (1 + np.exp(-v)) for v in x]
    x = np.reshape(x, x_shape)
    return x

def tanh(x):
    x_shape = x.shape
    x = np.reshape(x, [-1])
    x = [np.tanh(v) for v in x]
    x = np.reshape(x, x_shape)
    return x

• main.py

def plot_activation():
    x = np.arange(-10,10,1)
    out_relu = relu(x)
    out_leaky = leaky_relu(x)
    out_sigmoid = sigmoid(x)
    out_tanh = tanh(x)

    plt.figure(figsize=(10,5))
    output = {'out_relu':out_relu, 'out_leaky':out_leaky, 
                'out_sigmoid':out_sigmoid, 'out_tanh':out_tanh}
    key = list(output.keys())
    for i in range(len(key)):
        out = key[i]
        plt.subplot(2,2,i+1)
        plt.plot(x, output[out], 'o-')
        plt.title(out)
        plt.tight_layout()

    plt.show()

CNN 전체 구성

얕은 CNN을 프레임워크를 사용하지 않고, numpy로만 구성해보고자 한다.

layer는 다음과 같다.

• input : x [1,1,6,6]
• conv : w [1,1,3,3], k [3x3], stride=1, pad=0
• max pooling : k [2x2], stride=2, pad=0
• fc layer : w [4,1]
• L2 norm

역전파까지 진행해서 학습이 진행되는지를 볼 것이다. 역전파를 할 때는 chain rule을 사용하여 좀 더 간편하게 weight를 갱신한다.

max pooling을 역전파할 때는 다시 되돌리기 위해서는 max값을 가져온 위치를 알고 있어야 한다. 그것을 max unpooling 방식을 사용한다. 이를 통해 가져온 위치만 활성화하고, 나머지는 0으로 된다.

data, label, weight, h,w 선언

def shallow_network():
    # input [1,1,6,6], 2 iter
    x = [np.array(np.random.standard_normal([1,1,6,6]), dtype=np.float32),
         np.array(np.random.standard_normal([1,1,6,6]), dtype=np.float32)]
    # Ground Truth
    y = np.array([1,1], dtype=np.float32)
    

    # conv1 weights [1,1,3,3]
    w1 = np.array(np.random.standard_normal([1,1,3,3]), dtype=np.float32)
    # fc weights [1,4]
    w2 = np.array(np.random.standard_normal([1,4]), dtype=np.float32)

    lr = 0.01
    padding = 0
    stride = 1
    # L1 layer shape w,h
    L1_h = (x[0].shape[2] - w1.shape[2] + 2 * padding) // stride + 1
    L1_w = (x[0].shape[3] - w1.shape[3] + 2 * padding) // stride + 1

    print("L1 output : ({}, {})".format(L1_h, L1_w)) # (4, 4)

# -------------------- # 

L1 output : (4, 4)

• x,y : 1epoch마다 2번을 진행하기 휘애 2개를 선언해주었다. 이 때 나중에 값을 비교할 때 정확한 판단을 위해 dtype을 지정해줘야 한다. 따라서 array로 생성한다.
• conv1 weight : shape=[1,1,3,3] == [out_c, in_c, k_h, k_w]
• fc weight : shape=[1,4] == [1, n_classes]
• lr : learning rate
• stride : convolution에서는 1, pooling에서는 2
• L1_w, L1_h = convolution을 해서 나오는 출력 w, h

convolution, FC, pooling layer 선언

    # conv1
    Convolution = Conv(batch = x[0].shape[0],
                       in_c = x[0].shape[1],
                       out_c = w1.shape[0],
                       in_h = x[0].shape[2],
                       in_w = x[0].shape[3],
                       k_h = w1.shape[2],
                       k_w = w1.shape[3],
                       dilation = 1,
                       stride = stride,
                       pad = padding)

    # conv1 backprop conv
    Conv_diff =  Conv(batch = x[0].shape[0],
                      in_c = x[0].shape[1],
                      out_c = w1.shape[0],
                      in_h = x[0].shape[2],
                      in_w = x[0].shape[3],
                      k_h = L1_h,
                      k_w = L1_w,
                      dilation = 1,
                      stride = stride,
                      pad = padding)
    
    # max pooling
    Pooling = Pool(n_classes = x[0].shape[0],
                   in_c = w1.shape[1],
                   out_c = w1.shape[0],
                   in_h = L1_h,
                   in_w = L1_w,
                   kernel = 2,
                   dilation = 1,
                   stride = 2,
                   pad = 0)

    # FC
    Fc = FC(n_classes = 1,
            in_c = x[0].shape[1],
            out_c = 1,
            in_h = L1_h/2,
            in_w = L1_w/2)

• convolution
  • batch, in_c, in_h, in_w : input = [batch, in_c, in_h, in_w] 이므로 각각 지정
  • out_c, k_h, k_w : w = [out_c, in_c, k_h, k_w] 이므로 각각 지정

역전파에 사용될 convolution을 선언해준다. 자세한 내용은 아래에서 설명하겠다.

• conv_diff
  • k_h, k_w : 1 conv layer의 출력값으로 지정
• pooling
  • kernel,stride : pooling에서는 kernel size를 2로 설정하고, stride를 2로 설정하여 출력 크기를 1/2로 만듦
• FC
  • n_classes, out_c : 출력 크기는 n_classes x 1
  • in_c : 입력 채널
  • in_h, in_w : FC layer는 1 conv layer의 출력값에서 max pooling하여 1/2 크기가 된 값을 입력으로 받으므로 1/2해줘야 한다.

forward

    epochs = 100

    for e in range(epochs): # 100 epoch
        total_loss = 0
        for i in range(len(x)): # 2iter for each epoch
            # forward
            L1 = Convolution.gemm(x[i], w1)
            print (x[i].shape, w1.shape, L1.shape)

            L1_act = sigmoid(L1) # (1,1,4,4)
            
            L1_max = Pooling.maxpool(L1_act)

            #print (L1_max.shape) # (1,1,2,2)

            L1_max_flatten = np.reshape(L1_max, (1,-1))
            #print (L1_max_flatten.shape) # (1,4)

            L2 = Fc.fc(L1_max_flatten, w2)
            #print (L2.shape) # (1,1)
            #print (L2)

            L2_act = sigmoid(L2)
            #print (L2_act)

            loss = np.square(y[i] - L2_act) * 0.5
            total_loss += loss.item()
            #print (loss)

# -------------------- #

x1.shape : (1, 1, 6, 6), w1.shape : (1, 1, 3, 3), L1.shape : (1, 1, 4, 4)
L1_act.shape : (1, 1, 4, 4), L1_max.shape : (1, 1, 2, 2)
L1_max_flatten.shape : (1, 4)
L2.shape : (1, 1)

• epochs: 반복할 횟수 지정
• x의 길이만큼 반복
• forward
  1. 1 layer : conv layer
     • (b,in_c,in_h,in_w) * (out_c,in_c,k_h,k_w) = (b,out_c,out_h,out_w)
     • (1, 1, 6, 6) * (1, 1, 3, 3) = (1, 1, 4, 4)
     • out_h = (in_h - k_h + 2 * padding) // stride + 1
     • 4 = (6 - 3 + 2 * 0) // 1 + 1
  2. 1 layer activation
     • activation은 차원이 달라지지 않고, 값만 바뀐다.
  3. 1 layer max pooling
     • max pooling에서 stride와 kernel의 크기를 통해 결과의 크기를 설정할 수 있다.
     • 이 또한, out_h = (in_h - k_h + 2 * padding) // stride + 1
  4. 1 layer flatten
     • fc layer에 넣기 위해 1차원으로 변환시켜준다.
  5. 2 layer : fc layer
     • (n_classes, 1)
  6. 2 layer activation

backward

• w2 backpropagation

            # backward
            # delta E / delta w2
            diff_w2_1 = L2_act - y[i]

            diff_w2_2 = L2_act * ( 1 - L2_act)

            diff_w2_3 = L1_max

            diff_w2 = diff_w2_1 * diff_w2_2 * diff_w2_3
            #print (diff_w2) # 2x2 인데, fc layer.shape은 1x4이므로 변환해줘야 함

            diff_w2 = np.reshape(diff_w2, (1,-1))

# --------------- #
diff_w2_before.shape : (1, 1, 2, 2)
diff_w2_after.shape : (1, 4)

• diff_w2_1, diff_w2_2, diff_w2_3 : chain rule을 통해 $ \frac{\partial E}{\partial W_2} $ 를 구한다.

구한 diff_w2_1,2,3 을 곱해서 출력값을 구하면 (1,1,2,2) shape을 얻는다. 이는 w2를 최적화하는데 사용하는데 w2의 shape은 (1,4) 이므로 이를 변환시켜줘야 한다.

• w1 backpropagation

            # delta E / delta w1
            diff_w1_1 = diff_w2_1 * diff_w2_2
            #print (diff_w1_1.shape)
            diff_w1_2 = np.reshape(w2, (1,1,2,2)) # w2 [1,4] -> reshape
            #print (diff_w1_2.shape) # 1,1,2,2

            diff_w1_2 = diff_w1_2.repeat(2, axis=2).repeat(2, axis=3) # array를 n번 증폭
            #print (diff_w1_2.shape) # 1,1,4,4

            # diff maxpool
            diff_w1_3 = np.equal(L1_act, L1_max.repeat(2, axis=2).repeat(2, axis=3)) # pooling의 input, output,, 동일한 값의 인덱스를 구해줌, 동일한 행렬 크기로 만든 후 비교
            #print (diff_w1_3)

            diff_w1_4 = L1_act * (1- L1_act)
            #print (diff_w1_4.shape) # 1,1,4,4
            diff_w1_5 = x[i]

            diff_w1 = diff_w1_1 * diff_w1_2 * diff_w1_3 * diff_w1_4 

            # 위 4개의 결과는 4x4 이고, x[i]는 6x6이므로 x[i]에 conv를 진행해줘야 함
            diff_w1 = Conv_diff.gemm(x[i], diff_w1)
            
            #print (diff_w1)

chain rule에 의해 전개한 수식을 모두 곱하여 w1에 대한 diff를 구한다. 이 떄, 중요한 것은 diff_w1_5의 차원은 (1,1,6,6)인데, 나머지의 결과값들은 (!,1,4,4)이므로 이 둘을 곱하기 위해서 convolution 연산을 해야 한다. 그 이유는 6x6의 연소 개수는 36개인데, 이를 4x4에 reshape를 시켜줄 수 없다. 그러므로 연산을 위해 convolution을 진행한다.

            # update
            w2 = w2 - lr * diff_w2
            w1 = w1 - lr * diff_w1

        print("{} epoch loss {}".format(e, total_loss / len(x)))

# ----------------- #

0 epoch loss 0.18372559547424316
1 epoch loss 0.18269944936037064
2 epoch loss 0.18167604506015778

...

97 epoch loss 0.10186305642127991
98 epoch loss 0.101227305829525
99 epoch loss 0.10059575736522675

구한 가중치의 gradient를 통해 learning rate와 곱해서 가중치를 업데이트한다. 구한 total_loss는 x의 길이, 즉 반복한 횟수만큼 나눠주어 평균을 출력한다. loss가 줄어들고 있는 것을 확인할 수 있다.

FashionMNIST using Lenet5

지난 번에 만들어주었던 Lenet5를 사용하여 fashionMNIST를 학습시키고자 한다. 여기서 dropout, activation 변화 등을 추가했고, batch normalization 텀을 추가했다.

torch.nn.BatchNorm2d(num_features)

batch normalization에서 나머지 인자는 디폴트 값을 사용한다. 이는 conv layer와 activation 사이에 넣는다. fc layer에는 넣지 않는다.

class Lenet5(nn.Module):
    def __init__(self, batch, n_classes, in_channel, in_width, in_height, is_train = False):
        super().__init__()
        ...
        self.bn0 = nn.BatchNorm2d(6)
        self.bn1 = nn.BatchNorm2d(16)
        self.bn2 = nn.BatchNorm2d(128)

        self.dropout = nn.Dropout(p=0.3)

        # weight initialization
        torch.nn.init.xavier_uniform_(self.conv0.weight)
        torch.nn.init.xavier_uniform_(self.conv1.weight)
        torch.nn.init.xavier_uniform_(self.conv2.weight)
        torch.nn.init.xavier_uniform_(self.fc0.weight)
        torch.nn.init.xavier_uniform_(self.fc1.weight)


    def forward(self, x):
        x = self.conv0(x)
        x = self.bn0(x)
        x = torch.tanh(x)
        x = self.pool0(x)

        x = self.conv1(x)
        x = self.bn1(x)
        x = torch.tanh(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = self.bn2(x)
        x = torch.tanh(x)

        x = torch.flatten(x, start_dim=1)
        x = self.fc0(x)
        x = self.dropout(x)
        x = torch.tanh(x)
        x = self.fc1(x)
        x = x.view(self.batch, -1)
        x = nn.functional.softmax(x, dim=1) 

그 후 weight의 초기값을 설정하기 위해 weight initialization을 사용했다. 이에 대한 종류로는 torch.nn.init.xavier_ 들을 많이 사용한다. 이는 학습 데이터에서 통계를 기반으로 weight를 계산한다.

batchnorm만으로도 성능이 잘 나와서 dropout은 잘 사용하지 않으나, 성능 비교를 위해 마지막 layer에서 dropout을 함으로서 overfitting을 막을 수 있다. 만든 dropout은 fc layer에 추가한다.